DIEGO MARCONI

LA PHILOSOPHIE DU LANGAGE AU VINGTIÈME SIÈCLE

1. Réflexion philosophique sur le langage et « philosophie du langage ».

On peut dire que c’est au moins à partir du Cratyle de Platon, que la philosophie s’est occupée du langage : de son origine, de ses fonctions, du fondement de sa capacité à exprimer des significations ; et plus particulièrement des différentes « parties du discours » et de leurs fonctions, des différents types de relation sémantique, du rapport entre langage et pensée, langage et monde externe, langage et société humaine, et d’un très grand nombre d’autres problèmes à propos desquels le langage est pertinent. Elle s’en est occupée plus activement à certaines époques – vers la fin du Moyen Âge – et dans une moindre mesure à d’autres, comme par exemple entre le XVII^e et le XIX^e siècle (avec toutefois des exceptions remarquables, telles que Locke, Condillac et Humboldt) : ce qu’on peut dire, en tout cas, c’est que le langage n’est jamais complètement sorti du champ réflexif de la philosophie. Pourtant, lorsqu’on parle aujourd’hui de philosophie du langage, on se réfère habituellement à des études dont la bibliographie remonte rarement au-delà de 1892 (année de publication de Sens et dénotation de G. Frege). Certes, il peut arriver que des travaux plus anciens soient cités : la distinction leibnizienne entre intension et extension, son critère d’identité fondé sur la substituabilité salva veritate, la théorie « idéationnelle » de la signification proposée par Locke dans le livre III de son Essai sur l’entendement humain, ou la thèse de J. S. Mill selon laquelle la signification des noms propres se réduit à leur dénotation. On a toutefois l’impression que la référence à tel ou tel de ces classiques sert principalement à anoblir des positions contemporaines – en les dotant d’une tradition –, et que les noms de ces philosophes du passé fonctionnent comme les codes de thèses intemporelles, alors que le contexte de pensée dans lequel ces thèses ont été élaborées n’est d’aucune importance. À la différence de ce qui peut advenir dans d’autres secteurs de la philosophie contemporaine, comme l’éthique ou l’esthétique, les philosophes classiques, depuis Aristote jusqu’à Nietzsche, apparaissent dans la philosophie du langage comme autant de Statues du Commandeur, ou n’apparaissent pas du tout.

On peut donner différentes raisons plausibles de ce détachement, relativement profond et radical, de la « philosophie du langage » de la tradition philosophique. Avant tout, la « philosophie du langage » a instauré depuis ses origines, un rapport plutôt étroit avec la logique formelle, discipline scientifique qui n’existait quasiment pas avant Frege ; et la recherche la plus récente interagit souvent avec la linguistique, et particulièrement avec la linguistique générative, fondée par Chomsky à la fin des années cinquante (cf. § 3). Il faut toutefois préciser que ces deux interactions ne sont pas sans précédents : dans la philosophie de la fin du Moyen Âge, la relation entre logique et philosophie du langage était très étroite (une bonne part de la « logique » médiévale était plutôt de la philosophie du langage), et dans bon nombre de réflexions sur le langage entre le XVII^e et le XIX^e siècles (depuis la Logique de Port-Royal jusqu’à Humboldt) le rapport avec la linguistique est significatif. Toutefois, il est important qu’aujourd’hui, il s’agisse de logique formelle, mathématique, et de linguistique générative. En outre, comme nous le verrons (§ 2), la « philosophie du langage » est, par bien des côtés, interne à la tradition philosophique analytique : une tradition qui a certes des précédents importants dans l’histoire de la philosophie (il suffit de penser à Aristote ou à Hume), mais qui appartient pour l’essentiel à notre siècle. Enfin, une bonne partie de la réflexion philosophique qui aura précédé Frege ou le Tractatus logico-philosophicus de Wittgenstein est plus ou moins compromise (quelquefois malgré elle, quelquefois sous une forme théoriquement consentante) avec le mentalisme, qui reconduit les entités et les phénomènes linguistiques à des entités ou des processus mentaux. Nous assistons aujourd’hui à un retour significatif de thèses mentalistes également en « philosophie du langage », mais il ne fait pas de doute qu’à partir de Frege et pendant plusieurs décennies, la discipline s’est définie précisément en opposition au mentalisme (sur l’origine et les racines théoriques de cet anti-mentalisme, voir Engel, 1996 : 26-39, 69-89).

Enfin, une autre raison de ce détachement particulier de la philosophie du langage (au sens étroit) de la tradition philosophique tient au niveau de consensus atteint dans cette discipline. Bien plus que ce ne sera le cas pour l’éthique ou l’esthétique, les philosophes du langage sont convenus, si ce n’est d’un certain nombre de thèses philosophiques explicites, au moins de l’importance de certains problèmes et de la centralité de certains textes qui ont contribué à leurs discussions ; et ils sont également convenus d’une méthode de discussion (caractéristique de la philosophie analytique) difficilement définissable de manière précise, mais dans laquelle ont grand part les définitions et les argumentations explicites, l’emploi des contre-exemples pour invalider des propositions de solutions, le recours – non acritique, mais systématique – aux assomptions de sens commun et aux résultats des sciences naturelles et de la mathématique. Cet ensemble consensuel laisse certainement de côté, pour une raison ou pour une autre, une bonne partie des réflexions philosophiques sur le langage pré-frégéennes. D’un point de vue plus « historique », on pourrait dire que les classiques de la « philosophie du langage » – Frege, Russell, Wittgenstein – ont donné naissance à une telle masse de recherches qu’elle constitue, à elle seule, une discipline philosophique.

Ce qui ne veut pas dire que parmi ceux qui s’occupent aujourd’hui du langage d’un point de vue philosophique, le consensus – fût-il limité dans les termes que nous avons évoqués – soit universel, mais notre intention est de souligner de cette manière ce qui a été l’autorité particulière d’un ensemble relativement restreint de textes, qui constitue un cas peut-être unique dans le panorama de la philosophie contemporaine. On comprendra sans doute mieux, de ce point de vue, le rapport difficile et l’absence substantielle de dialogue entre la « philosophie du langage » et les courants actuels de l’herméneutique, qui placent pourtant le langage au centre de leur préoccupation (« L’être qui peut être compris, c’est le langage » dit Gadamer ; et il ajoute que « le langage, et donc la compréhension, sont des caractères qui définissent en général et fondamentalement tout rapport de l’homme avec le monde ». Voir Gadamer, 1960 : 405 q.). Les différences de style philosophique sont évidentes ; mais, cela mis à part, les problèmes de la philosophie analytique du langage sont substantiellement étrangers à l’herméneutique. On chercherait en vain, dans les écrits des herméneutes, des réponses à des questions telles que : « De quelle manière le sens d’une phrase déclarative dépend des sens de ses constituants ? » ou : « Quelle différence y a-t-il entre le sens d’une expression comme “je” et celui d’une expression comme “Napoléon Bonaparte” ? », ou : « Est-il toujours vrai que le sens d’une expression détermine sa référence ? ». De telles questions sont considérées soit comme banales (la réponse en est évidente), soit comme dépourvues de caractère philosophique ou, tout au plus, d’un intérêt strictement linguistique (§ 3), ou encore mal formulées. Les emplois quotidiens ou ordinaires du langage, qui sont au centre de l’attention de la philosophie du langage (parce que c’est de là qu’il faut partir) n’intéressent pas les herméneutes, qui tendent à les considérer comme dégradés par rapport à des emplois plus révélatifs de l’être ou de la vérité. Les herméneutes emploient certainement des notions comme sens ou signification : mais ce que la tradition analytique considère comme le centre de la signification – ce que Carnap (1947 : 6) appelait « signification cognitive » et dont Frege (1892b : 104) disait que, d’une langue à l’autre, elle était conservée par une traduction correcte – intéresse bien moins les herméneutes que d’autres aspects, considérés comme marginaux ou secondaires par les philosophes du langage. Ces derniers s’intéressent plutôt à ce que des mots tels que « cheval » ou « destrier » ont en commun ; les herméneutes à ce qui les différencie. « L’esprit orienté vers la beauté de la langue pourra accorder de l’importance à ce que le logicien considérera comme indifférent » (Frege, 1918 : 178).

2. Philosophie du langage et philosophie linguistique

Le programme de recherche de la philosophie du langage – désormais sans guillemets, dans la mesure où nous n’en parlerons qu’au sens restreint évoqué ci-dessus – est quelquefois identifié avec le mot d’ordre : « Les problèmes philosophiques sont des problèmes de langage » ; et les expressions “philosophie du langage” et “philosophie linguistique” sont souvent utilisées comme des synonymes. Pourtant, cette identification est, aujourd’hui, une erreur : la majeure partie des philosophes du langage ne pensent nullement que les problèmes philosophiques de la justice, de la justification des théories scientifiques, de la nature de l’art ou du rapport entre le corps et l’esprit soient, en tout cas essentiellement, des problèmes de langage (en aucun des sens que nous éclaircirons bientôt). Toutefois, cette erreur se justifie historiquement : la plupart des recherches philosophiques sur le langage dont nous nous occuperons, sont nées, de fait, à l’enseigne d’un tel mot d’ordre, qui continuera de caractériser la recherche au moins jusqu’à la fin des années cinquante. Selon une première interprétation, ce mot d’ordre revient à dire que les problèmes philosophiques naissent du langage : de ses imperfections, de son opacité et de la méprise quant à sa manière de fonctionner. Les recherches de Frege sont déjà en partie motivées par la conviction que le langage naturel est une source quasi inévitable de « tromperies » (Frege, 1879 : VI), et qu’à toute fin scientifique, il doit être remplacé par une langue artificielle (telle que l’« idéographie » qu’il propose), qui est à la langue naturelle ce que le microscope est à l’œil (1879 : V). Bien plus tard, Wittgenstein, aurait soutenu que « les confusions les plus fondamentales (dont la philosophie [traditionnelle, bien entendu] est pleine » naissent de la méprise quant à la manière dont fonctionne le langage ordinaire (1922, 3.323-3.324), et que « toute la philosophie [nouvelle, à laquelle Wittgenstein se propose de contribuer] est une «critique du langage » (4.0031). Dans la formation de ces idées de Wittgenstein, entra pour une grande part l’enseignement de Russell (§ 9) sur la nécessité de distinguer entre « forme grammaticale » d’un énoncé et « forme logique », à savoir entre ce qu’un énoncé semble dire et ce qu’il dit effectivement. De telles positions sont à l’origine d’une tendance de la philosophie linguistique (que nous appellerons « dissolutive » ou « thérapeutique »), selon laquelle les problèmes philosophiques sont des problèmes de langage, au sens où ils sont engendrés par le langage naturel, et il revient à la philosophie non pas de les résoudre mais de les éliminer, soit à travers une compréhension claire et explicite de la manière dont le langage fonctionne (au-delà de son apparence grammaticale trompeuse), soit, plus drastiquement, en remplaçant le langage naturel par un langage artificiel parfait, dans lequel les problèmes philosophiques ne seraient pas formulables, ou alors seraient reformulés en tant que problèmes scientifiques légitimes. Cette tendance dissolutive, dont on peut dire que le Tractatus est le manifeste, est présente dans le premier néo-positivisme, dans une bonne partie de la philosophie anglaise des années trente (de manière typique chez G. Ryle) et dans le « second » Wittgenstein (§ 19-22), pour qui la réhabilitation du langage ordinaire n’entraîne nullement une réhabilitation de la philosophie traditionnelle.

Mais le mot d’ordre : « Les problèmes philosophiques sont des problèmes de langage » a fait également l’objet d’une autre interprétation : les problèmes philosophiques sont des problèmes de signification des mots, et se résolvent en vérifiant la signification de certains mots. Se demander ce qu’est la connaissance, ou ce qu’est la justice, revient à se demander quelle est la signification de mots tels que « connaître » ou « juste ». D’après Schlick, qui fut un défenseur de cette version de la philosophie linguistique (cf. Schlick, 1932), déjà Socrate avait compris qu’il ne s’agit pas en philosophie de vérifier des faits, comme dans les sciences, mais de clarifier des significations. Les problèmes philosophiques sont des problèmes de langage au sens où ils concernent le langage, et se résolvent à travers l’analyse du langage. Ceux qui soutiennent cette position – « résolutive » ou constructive – n’excluent pas nécessairement l’utilité des langages artificiels « parfaits », mais ils considèrent le plus souvent le langage ordinaire comme le lieu de résolution des problèmes philosophiques. Le représentant le plus célèbre de cette version de la philosophie linguistique sera Austin (§ 24-25) : la vérification analytique de l’utilisation des mots n’est pas la réponse finale à tous les problèmes philosophiques, mais elle est un point de départ infiniment plus riche et mûr que toutes les alternatives possibles.

Les deux versions de la philosophie linguistique que nous avons distinguées ici se sont de fait mêlées de multiples manières (Rorty, 1967, fait une analyse précise de ces événements). Aujourd’hui, la philosophie linguistique n’existe plus : la tendance dissolutive – qui a pourtant laissé un important héritage en terme de méfiance à l’égard des formulations typiques de la philosophie dite traditionnelle – a été vaincue par la conviction que de nombreux problèmes philosophiques peuvent être reformulés en termes clairs et tout à fait acceptables ; la tendance constructive s’est effondrée, accusée de penser – de manière absurde – que des questions substantielles, pour la résolution desquelles est pertinente la connaissance de comment sont les choses dans le monde, peuvent être résolues à travers l’analyse du langage (l’attaque de Putnam [Putnam, 1962] contre Malcolm est exemplaire d’une telle critique). Mais l’attaque de Quine contre la notion de signification, à travers la critique de la dichotomie analytique/synthétique, n’en fut pas moins importante pour le déclin de la version constructive (§ 27 ; Rorty [1979 : 193 et passim] a justement insisté sur l’efficacité destructrice de la critique de Quine). S’il n’est pas possible d’isoler, à l’intérieur du langage, les énoncés qui sont constitutifs de la signification d’un mot de ceux qui ne le sont pas, le programme philosophique qui se propose de vérifier le contenu d’un concept (tel que « justice », « connaissance », etc.) à travers l’analyse de la signification d’un mot (“juste”, “connaître”) doit être à tout le moins reconsidéré.

Mais la philosophie linguistique a laissé un héritage théorique considérable, qui constitue, en bonne part, le patrimoine des idées de la philosophie du langage. Dans la poursuite d’un objectif qui – comme on l’a dit – n’était pas, en dernière analyse, de réflexion sur le langage, mais de résolution (ou de dissolution) des problèmes de la philosophie en général, les philosophes linguistiques ont élaboré des concepts et des théories sur le langage qui ont encore cours aujourd’hui. Par exemple, le couple frégéen de sens et dénotation (§ 5) fut introduit pour éliminer la confusion, fréquente en philosophie des mathématiques, entre signe, sens du signe et objet désigné par le signe (cf. Picardi, 1989 : 332) ; l’analyse des descriptions définies par Russell (§ 9) devait servir à résoudre le problème posé par les « entités inexistantes » (par exemple “l’actuel roi de France”, “la montagne d’or”, “Pégase”), et donc un problème ontologique ; la théorie des performatifs d’Austin (§ 25) se forma au cours d’une discussion sur les problèmes de l’esprit d’autrui (Austin, 1946 : 45 sq.) et de la vérité (Austin, 1950 : 92 sq.). Il est probable que nombre d’idées sur le langage ne seraient pas nées si elles n’avaient pas paru utiles pour traiter d’autres problèmes philosophiques. Aujourd’hui, elles sont utilisées la plupart du temps pour comprendre philosophiquement le langage, indépendamment d’objectifs « externes ». Des positions telles que celle de Dummett (voir par exemple 1973a), qui assigne à la philosophie du langage un rôle fondateur par rapport à l’ensemble de la philosophie, sont nettement minoritaires.

3. Philosophie du langage et linguistique

S’il est vrai que la philosophie du langage a évolué dans le sens d’une compréhension propre de ce qu’est le langage et de comment il fonctionne, on peut se demander si elle n’est pas devenue en tout point identique à la linguistique, ou à l’une de ses parties. On pourrait répondre aisément – mais à tort – que la linguistique, au contraire de la philosophie, ne s’occupe pas « du langage », mais des langues historico-naturelles, objets individuels ayant chacun leur histoire, certaines régularités de mutation, une structure. En premier lieu, en effet, les idiosyncrasies des différentes langues ne sont pas nécessairement sans conséquence pour la philosophie du langage : c’est précisément dans la mesure où elle tend à établir des conclusions générales, qu’il n’est pas indifférent que celles-ci soient contredites par des phénomènes linguistiques spécifiques de telle ou telle langue. En second lieu, il existe une linguistique théorique, ou générale, qui considère les langues historico-naturelles essentiellement comme le matériau empirique d’une théorie générale du langage verbal. « En dernière analyse, le linguiste n’est pas intéressé par la connaissance du français, de l’arabe, ou de l’anglais, mais par la faculté linguistique de l’espèce humaine » écrit une linguiste contemporaine (Cook, 1988 : 22).

Prenons, à titre d’exemple, le programme de recherche de Noam Chomsky. La tâche centrale de sa théorie linguistique est la description de la grammaire universelle : elle consiste en un ensemble de composants et principes invariants dans toutes les langues, et de paramètres qui admettent un nombre limité de valeurs possibles (par exemple, dans un syntagme les compléments peuvent suivre ou au contraire précéder la tête ; l’ordre des constituants de la phrase peut être S[ujet]-V[erbe]-O[bjet], ou SOV, ou VSO). Les grammaires des différentes langues dérivent de différents choix de spécification des paramètres. Par ailleurs, les choix ne sont pas tous indépendants : dans de nombreux cas, si un paramètre a une certaine valeur, d’autres s’en trouveront déterminés. Par exemple, si, dans une langue, l’ordre des constituants est VSO, les adjectifs suivront les noms au lieu de les précéder. La grammaire universelle est une théorie de la faculté du langage, le module – relativement isolé – de l’esprit humain réservé à la connaissance linguistique : les principes de la grammaire universelle devraient, normalement, pouvoir être mis en relation avec les caractéristiques physiques du cerveau.

Ces quelques remarques suffisent à mettre en évidence les ambitions d’universalité du programme de Chomsky ; ambitions qui, par ailleurs, ne sont pas la prérogative exclusive de la linguistique générative. La philosophie du langage ne peut donc être distinguée de la linguistique en vertu de son aspect théorique plutôt qu’historique, ni de son intérêt pour le langage en général plutôt qu’aux différentes langues ou à des groupes de langues, ou du fait qu’elle est « pure » et non pas empirique ; et elle ferait bien de ne pas s’en distinguer en ignorant les phénomènes linguistiques et les particularités des différentes langues. Le rapport entre les deux domaines de recherche est plus complexe, et ne peut être éclairé qu’à partir de certaines considérations de caractère historique.

On a vu que la philosophie linguistique, sous toutes ses formes, est dominée par des préoccupations philosophiques extra-linguistiques. En conséquence, elle s’est souvent engagée dans des analyses qui eurent une grande importance pour la philosophie, mais sans véritable enjeu linguistique : il est clair que le rôle de l’adjectif “volontaire” (Ryle, Austin) n’intéresse que de manière très relative la linguistique, pas plus que celui de l’énoncé “j’ai mal” (Wittgenstein) ; la linguistique ne s’occupe pas des expressions particulières, mais des classes d’expressions. En outre, une bonne partie de la philosophie linguistique, au cours de toute sa première phase, a été dominée par la méfiance à l’égard du langage naturel. Nous avons vu (§ 2) que cette attitude pouvait être commune à Frege et au « premier » Wittgenstein ; plus tard, les résultats de Tarski (§ 13) sur le caractère contradictoire des théories formulées dans un langage sémantiquement clos (comme le sont toutes les langues naturelles) semblaient sonner le glas de toute velléité de traitement rigoureux du langage naturel. À l’anarchie des langages naturels s’opposaient la discipline et la transparence des langages logiques. Pour des philosophes qui – comme le sont nombre de philosophes linguistiques – avaient à cœur la libération de la philosophie et de la science, des obscurités et des confusions du langage naturel, et la mise en fonction d’un instrument linguistique optimal, tant pour l’analyse philosophique que pour les discours scientifiques, la théorie du langage était avant tout une théorie des langages artificiels de la logique, opportunément enrichis pour en accroître le pouvoir expressif (sur le thème du « langage idéal » dans la philosophie linguistique, voir également Rorty, 1967). Toute la première phase de la pensée de Carnap, depuis la Construction logique du monde (1928) jusqu’à la Syntaxe logique du langage (1934) se développe dans cet esprit. On peut même affirmer, sans exagération, que depuis Frege jusqu’à la fin des années soixante-dix, la théorie des langages logiques a une fonction paradigmatique pour quasiment toute la philosophie du langage. Ce qui ne veut pas dire que cette attitude impliquait un refus pur et simple du langage naturel dans tous les cas (ce n’est pas le cas, par exemple, du Tractatus de Wittgenstein) ; mais par rapport à celui-ci, les théories du langage finissaient par assumer, explicitement ou implicitement, un rôle prescriptif plutôt que descriptif : soit en opposant au langage naturel des langages dotés de propriétés idéales (comme chez Frege, le premier Carnap ou Tarski), soit en lisant en filigrane dans le langage naturel un langage parfait – essentiellement logique – duquel les langues naturelles étaient souvent éloignées en surface (comme chez Russell et dans le Tractatus). Par conséquent, les théories du langage élaborées par ces philosophes ne représentaient que rarement et indirectement un enjeu pour la linguistique qui, évidemment, se doit de prendre en compte tous les traits d’« indiscipline » présumée des langues naturelles. Quand les philosophes se sont occupés véritablement du langage naturel, et ils le firent avec des intentions descriptives, ils ont élaboré des théories qui appartiennent tout autant à linguistique qu’à la philosophie, comme la théorie des actes de langage (§ 25) ou la grammaire de Montague (§ 17).

Par ailleurs, la philosophie du langage s’est différenciée de la linguistique également pour une raison, en un certain sens, opposée, à savoir de par son engagement théorique sur des aspects de la connaissance du langage dont la linguistique reconnaissait l’importance, mais qu’elle ne réussissait pas à occuper de manière satisfaisante : avant tout la sémantique, ou théorie de la signification. De la linguistique historique au structuralisme de Saussure, de Jakobson à Chomsky, la linguistique a toujours considéré comme de son ressort la problématique de la signification linguistique ; toutefois, aucune théorie élaborée à cet égard, dans un cadre linguistique, n’est parvenue au degré de maturité des théories phonologiques ou syntaxiques. Cette lacune a été largement comblée par la philosophie du langage et on en comprendra facilement les raisons : tout d’abord, le problème de la signification appartient à la tradition philosophique, depuis le stoïcisme (au moins) ; ensuite, les problèmes philosophiques qui intéressaient les philosophes linguistiques se posaient comme des problèmes de la signification de certains mots ou de certaines phrases, et sollicitaient, pour être affrontés de manière adéquate, une théorie de la signification des mots et des phrases (on trouvera d’importantes analyses des origines de la « sémantique philosophique » dans Hacking, 1975 ; Dummett, 1988). La philosophie du langage a donc fonctionné comme suppléance par rapport à la linguistique dans l’aire de la théorie sémantique, et elle fut, en même temps, le lieu principal de la discussion méthodologique et épistémologique la concernant. Différents philosophes ont soutenu qu’une des tâches historiques de la philosophie a été, et est encore la construction d’un consensus autour de clusters conceptuels, dont on peut dire que l’adoption généralisée a pu donner naissance à une science : c’est ainsi que sont nées la mécanique classique et la psychologie (Russell 1912 : 154-155 ; Perelman, 1945 : 13). Il est possible qu’un jour nous réalisions que la fonction principale des réflexions philosophiques sur le langage aura été de donner naissance à une sémantique scientifique (qui serait une partie de la linguistique, même si ce ne sera peut-être pas celle que nous connaissons aujourd’hui). Toutefois, si ce devait être le point d’arrivée, nous en sommes encore bien loin, comme nous le verrons.

4. Le paradigme dominant

Le paradigme dominant de la philosophie du langage au XX^e siècle peut être caractérisé par la conjonction de trois thèses, deux positives et une négative :

1) la signification d’un énoncé déclaratif s’identifie avec ses conditions de vérité, soit, en d’autres termes, la spécification des circonstances dans lesquelles l’énoncé est vrai ; et la signification d’une expression subénonciative (par exemple un mot) est sa contribution aux conditions de vérité des énoncés dans lesquels l’expression apparaît. L’énoncé déclaratif est donc l’unité linguistique privilégiée : la théorie sémantique est essentiellement une théorie de la signification des énoncés ;

2) la valeur sémantique d’une expression complexe dépend fonctionnellement des valeurs sémantiques de ses constituants (compositionnalité de la signification) ; le mode de la dépendance est déterminé par la structure syntaxique de l’expression complexe, c’est-à-dire par le type de complexité qui est en jeu dans chaque cas ;

3) images, représentations, ou autres entités mentales, éventuellement associées aux expressions linguistiques, ne sont pas les significations des expressions, et l’élaboration mentale des expressions linguistiques (la compréhension comme processus mental) n’est pas essentielle à la détermination de la signification des expressions elles-mêmes. En général, des considérations de caractère psychologique n’interviennent pas dans la théorie de la signification.

L’idée selon laquelle, pour satisfaire les thèses (1) et (2), on doit attribuer plusieurs valeurs sémantiques à chaque expression linguistique (par exemple sens et dénotation chez Frege, ou intension et extension chez Carnap) est presque aussi universellement partagée. Russell (§ 9) n’était pourtant pas de cet avis, pas plus que ne le sont aujourd’hui les théoriciens de la référence directe (§ 32), qui se placent d’ailleurs déjà partiellement en dehors du paradigme dominant.

Les thèses (2) et (3) sont dues à Frege. La thèse (1) déjà présente chez Frege (1893, § 32), est soulignée avec force dans le Tractatus de Wittgenstein.

5. La philosophie du langage de Frege : termes singuliers

Gottlob Frege (1848-1925) était bien conscient d’être l’un des fondateurs de la logique contemporaine. Il était loin pourtant de penser que, quelques dizaines d’années après sa mort, on l’aurait également considéré comme le fondateur d’une discipline philosophique dite « philosophie du langage » : ne serait-ce que parce qu’il s’était toujours considéré plus comme mathématicien que comme philosophe. Toutefois, cela ne fait aucun doute que nous sommes redevables à Frege des notions centrales du paradigme dominant, comme l’analyse de la prédication et des énoncés quantifiés, de l’idée de la compositionnalité de la signification et du couple sens/dénotation ; et ce fut Frege qui, le premier, posa des problèmes canoniques, tels que celui de la signification des descriptions définies (les expressions de la forme “le P”, comme “le roi de France” ou “la tante de Gottlob”) ou celui des contextes d’attitude propositionnelle (“X croit que que”, “X veut savoir si p” etc.). La grande synthèse de Dummett (1973b) a sans aucun doute contribué à l’image actuelle du rôle de Frege dans la constitution de la philosophie du langage ; d’autre part, c’est un fait que quasiment tous les auteurs canoniques de la philosophie du langage de notre siècle se réfèrent à lui, depuis Russell qui contribua à en diffuser les idées, jusqu’à Wittgenstein qui reconnut qu’il fut l’un des rares auteurs à avoir exercé une influence importante sur sa pensée, ou Carnap qui fut son élève et qui tenta d’en perfectionner les catégories sémantiques, ou encore Austin qui le traduisit en anglais, et Quine qui hérita de nombres de ses problèmes, jusqu’à Kripke qui en fit la cible de ses polémiques.

Une grande partie des idées sémantiques de Frege est exposée dans trois courts essais des années 1891-1892, Fonction et concept, Sens et dénotation, Concept et objet. Frege appelle “noms propres” ce que nous appelons aujourd’hui généralement termes singuliers, c’est-à-dire les expressions linguistiques qui désignent un seul objet (par exemple “Clichy-sous-bois”, “l’homme le plus riche de Clichy-sous-bois”, “Alfred Biquet”). À chaque nom propre sont associés, selon Frege, un sens (Sinn) et une dénotation (Bedeutung). La dénotation du nom, c’est l’objet désigné : dans l’exemple, respectivement, la ville de Clichy-sous-bois, l’homme qui, dans cette ville, se trouve être le plus riche, celui qui porte le nom “Alfred Biquet”. Le sens est « le mode selon lequel l’objet est donné » par le nom (1892b : 105) ; il peut être conçu comme le contenu cognitif associé au nom, en vertu duquel il a telle dénotation ; c’est-à-dire comme un des différents modes selon lequel un objet peut être déterminé, en tant qu’il « donne lieu à un nom particulier » de cet objet (Frege, 1914 : 107). Il s’agit d’une notion problématique (§ 32), que Frege lui-même ne clarifie qu’en partie. Essayons d’en dessiner les contours dans la mesure du possible. Avant tout, il est clair qu’un même objet peut être désigné par plusieurs expressions linguistiques, chacune desquelles constituant un « parcours » spécifique pour parvenir à cet objet. L’actuelle (1997) reine d’Angleterre peut être désignée par l’expression “Elizabeth II”, ou par l’expression “l’ex-belle-mère de Diana Spencer”, ou par un grand nombre d’autres expressions (parmi lesquelles précisément “l’actuelle reine d’Angleterre”). Chacune de ces expressions présente sa dénotation (qui est la même dans tous les cas) d’une manière spécifique, qui est son sens. Pourquoi ne nous suffit-il pas (selon Frege) de dire que des expressions différentes (des noms différents) ont la même dénotation, au lieu de devoir associer à chaque expression un sens, c’est-à-dire un mode selon lequel elle présente sa dénotation ? La réponse, toujours selon Frege, est que les mots, considérés comme de simples signes, ne sont pas des instruments de connaissance, ni des véhicules de la communication : ils ne le deviennent qu’en tant qu’ils sont associés à une dénotation. Le sens d’une expression n’est autre que le mode particulier selon lequel elle renvoie à sa dénotation.

Deux expressions distinctes peuvent avoir le même sens : ainsi le sens n’est pas une autre manière de nommer ce par quoi une expression linguistique se différencie d’une autre. Carnap reprochera à Frege de n’avoir pas été assez précis sur les conditions d’identité par le sens (§ 14 ; voir Casalegno, 1992 : 25-26) ; toutefois, il ne fait pas de doute (1892a : 127-140 ; 1892b : 106, 107-108) qu’il pensait qu’il pouvait y avoir des expressions distinctes avec le même sens, à la fois dans des langues différentes (“horse”, “cheval” et “cavallo” ont le même sens), et à l’intérieur d’une même langue (“chien” et “clébard”, “cheval” et “destrier”, “et” et “mais” ont le même sens, 1897 : 139, 152 ; 1918 : 177-178). Ces derniers exemples sont des mots qui, bien qu’ayant le même sens, ont une tonalité différente (Frege, 1918 : 177). La tonalité est ce qui se perd généralement dans une traduction d’une langue vers une autre (qui, si elle est correcte, doit au contraire conserver le sens).

Du sens d’une expression linguistique il faut distinguer la représentation liée à l’expression, c’est-à-dire l’entité mentale que l’expression peut évoquer dans notre esprit : « Une image interne qui s’est constituée sur la base des souvenirs des impressions sensibles que j’ai éprouvées et d’activités, internes et externes, que j’ai effectuées » (Frege, 1892b : 105). Les représentations sont inévitablement subjectives : chacun de nous associe à une même expression une représentation différente, parce que la représentation dépend de l’expérience, et l’expérience est différente selon les individus. « S’il était possible de projeter sur un écran les représentations évoquées par le mot “cheval” chez des personnes différentes, nous verrions des images très différentes les unes des autres » (1897 : 151). Mais le langage doit être capable d’exprimer un contenu objectif – un sens – pour que la communication soit possible. Afin que l’on puisse communiquer réciproquement un contenu de connaissance – par exemple le théorème de Pythagore – à travers le langage, il faut qu’un sens, qui soit le même pour tous, soit lié à chacun des mots du théorème (sans quoi « il faudrait dire “mon théorème de Pythagore” ou “ton théorème de Pythagore” et non plus «le théorème de Pythagore » : Frege, 1918 : 183). Ce qui ne veut pas dire, bien entendu, que des personnes différentes ne puissent accorder des sens différents à une même expression (pour untel le sens d’“Aristote” peut être « le maître d’Alexandre le Grand », pour un autre « le philosophe de Stagire, auteur de la Métaphysique ») : toutefois il est possible qu’il y ait des expressions avec un sens déterminé, qui soit saisi par tous les utilisateurs de langage, tandis qu’il n’est pas possible que tous associent à une expression la même représentation. Et cela ne veut pas dire non plus que le fait de saisir un sens ne soit pas un événement mental (ou, disons, un fait psychologique) : mais le sens même, ce qui est saisi par l’esprit, n’est pas soumis à la subjectivisation, caractéristique des événements mentaux.

Les rapports entre sens, dénotation et représentation sont bien mis en évidence par Frege par une métaphore. Imaginons quelqu’un qui observe la Lune à travers une lunette. La Lune elle-même correspond à la dénotation ; l’image rétinienne, qui est différente selon les observateurs, correspond à la représentation ; l’image sur la lentille de la lunette correspond au sens : « Elle en est nécessairement partiale parce qu’elle dépend du point de vue d’observation, et pourtant elle est objective, parce qu’elle peut servir à plusieurs observateurs » (1892b : 106).

L’imperfection du langage naturel (dont Frege sera un critique acharné) permet la formation d’expressions anomales, qui ont un sens mais pas de dénotation, comme “le corps céleste le plus éloigné” ou “le plus grand nombre naturel”. Dans un langage parfait cela ne devrait pas être possible : on ne pourrait pas introduire ou former de signe sans que lui soit garantie une dénotation (1892b : 109). Au contraire, dans le langage naturel, nous parlons d’une certaine façon en présupposant que les termes singuliers que nous employons ont une dénotation. En disant, par exemple, “Kepler mourut dans la misère” ou “Celui qui a découvert les orbites elliptiques des planètes mourut dans la misère”, nous présupposons, respectivement, que le nom “Kepler” a une dénotation et que quelqu’un a découvert la forme elliptique des orbites des planètes. Si le présupposé est faux (comme c’est le cas dans des énoncés tels que “Ulysse a exterminé les Guaranis” ou “L’actuel roi du Mexique a gagné le tour de France”), ni l’énoncé, ni sa négation ne sont vraies : les présupposés en question, en effet, conditionnent de la même manière les valeurs de vérité des énoncés et ceux de leurs négations (même en disant “Ulysse n’a pas exterminé les Guaranis” on présuppose que le nom “Ulysse” a une dénotation). Nous verrons (§ 9) comment Russell refusera cette analyse, qui implique une violation du principe du tiers exclu.

6. Les énoncés et le principe de compositionnalité

Les énoncés (déclaratifs) ont également un sens et une dénotation : le sens d’un énoncé est la pensée qu’il exprime, sa dénotation est sa valeur de vérité (c’est-à-dire le Vrai, si l’énoncé est vrai, ou le Faux, s’il est faux). Dans l’argumentation à laquelle Frege a recours pour arriver à cette conclusion, il fait appel à un principe qui est tout aussi important que le résultat auquel il parvient : ledit principe de compositionnalité, selon lequel la valeur sémantique (sens ou dénotation) de toute expression complexe est fonction des valeurs sémantiques de ses constituants.

Voyons l’argumentation de Frege. Il constate qu’un énoncé exprime une pensée, et se demande si la pensée exprimée peut être la dénotation de l’énoncé. S’il en était ainsi – dit-il – la pensée exprimée ne devrait pas changer, là où, dans l’énoncé, on remplace une partie par une autre de même dénotation. Cette affirmation présuppose le principe de compositionnalité. En effet, étant donné A {e₁, ... e_n} un énoncé dont les constituants sont e₁, ..., e_n. Nous désignons par “den(x)” la dénotation de l’expression “x”. Si le principe

den (A {e₁, ... e_n}) = f (den (e₁), ..., den(e_n))

[principe de compositionnalité pour la dénotation], est valable, alors, si nous avons par exemple

den (e_i) = den (e_j)

nous aurons de toute évidence

den (A{e₁, ..., e_i, ..., e_n}) = den (A{e₁, ..., e_j, ..., e_n}),

où l’énoncé A conserve sa dénotation si l’on remplace e_i par e_j. Mais si la dénotation était la pensée, cela ne pourrait être le cas. Considérons, par exemple, l’énoncé :

(1) L’étoile du matin est un corps illuminé par le Soleil.

Si nous remplaçons “l’étoile du matin” par “l’étoile du soir” (qui a la même dénotation : tous deux dénotent la planète Vénus), nous obtenons

(2) L’étoile du soir est un corps illuminé par le Soleil,

qui exprime une pensée différente de (1). Donc, si la dénotation respecte le principe de compositionnalité, la dénotation d’un énoncé ne peut être la pensée exprimée.

Pour soutenir sa thèse selon laquelle la dénotation est la valeur de vérité, Frege apporte deux argumentations de type inductif. La première part de la constatation que nous sommes intéressés par la dénotation des constituants d’un énoncé lorsque nous avons intérêt à savoir si l’énoncé est vrai ou faux et seulement dans ce cas. Par exemple, nous ne sommes pas intéressés de savoir si “Ulysse” a une dénotation – c’est-à-dire si Ulysse a existé – quand nous restons dans le cadre de l’Odyssée, à savoir un contexte fictif, où la vérité ou l’absence de vérité des énoncés n’est pas en question ; le fait nous intéresse au contraire, si nous nous plaçons dans le cadre d’une recherche historique. Ce qui fait penser (en assumant une nouvelle fois le principe de compositionnalité) que la valeur de vérité est précisément ce qui est déterminé par les dénotations des constituants d’un énoncé, à savoir la dénotation de l’énoncé tout entier.

La seconde argumentation part au contraire de l’observation que la valeur de vérité d’un énoncé ne change pas quand on remplace des constituants de même dénotation : (1) et (2) ont la même valeur de vérité (ils sont tous les deux vrais). Bien sûr, nous ne savons pas si la valeur de vérité est la seule propriété d’un énoncé qui ne varie pas dans ce cas. Mais le principe de compositionnalité nous dit que la dénotation d’un énoncé est quelque chose qui ne change pas par substitution des constituants de même dénotation : donc la valeur de vérité, ayant cette propriété d’invariance, est un candidat légitime (au contraire de la pensée exprimée) à l’identification avec la dénotation de l’énoncé.

La thèse selon laquelle la dénotation d’un énoncé déclaratif est sa valeur de vérité a une conséquence bizarre : tous les énoncés vrais, et tous les énoncés faux, ont la même dénotation. Frege n’esquive pas cette conséquence (1892b : 111), et l’interprète ainsi : d’un énoncé, ne nous intéresse jamais la seule dénotation, mais le mode particulier selon lequel il dénote cette valeur de vérité déterminée. « La connaissance est dans la connexion de la pensée avec sa dénotation, à savoir avec sa valeur de vérité. » Que tous les énoncés vrais aient la même dénotation ne veut certainement pas dire que leur différence soit en quelque manière banale et qu’ils soient, dans un certain sens, un seul et même énoncé : ils sont des manières différentes de « décomposer » la même valeur de vérité.

Le principe de compositionnalité – qui, comme on l’a vu, est essentiel dans l’argumentation de Frege – est au fondement d’une bonne partie de la recherche sémantique contemporaine. L’une de ses motivations les plus importantes est la suivante : il serait difficile de concevoir, sans admettre un principe de compositionnalité de la signification, que l’on puisse comprendre des phrases que nous n’avons jamais entendues – sans qu’elles nous soient expliquées –, à la seule condition qu’elles soient constituées de mots que nous connaissons. Évidemment, nous calculons la signification des expressions nouvelles à partir des significations de leurs sous-expressions, que nous connaissons déjà. La signification d’une expression complexe est, en ce sens, fonction des significations de ses constituants : la connaissance des significations des constituants suffit à déterminer, sur la base de la structure syntaxique de l’expression, la signification de l’expression complexe. Frege exprimait ainsi l’idée de la compositionnalité (en ce cas, du sens) : « Les prestations de la langue sont vraiment surprenantes : exprimer un très grand nombre de pensées avec peu de syllabes – ou même trouver la manière de donner à une pensée [...] une mise qui permette qu’un autre, pour lequel elle est absolument nouvelle, la reconnaisse. Cela ne serait pas possible si nous ne pouvions distinguer dans la pensée des parties auxquelles correspondent des parties de l’énoncé, de manière à ce que la construction de l’énoncé puisse valoir comme image de la construction de la pensée » (Frege, 1923-1926 : 36).

Le sens d’un énoncé c’est la pensée qu’il exprime. Les pensées, comme les sens des termes singuliers, ne doivent pas être conçues comme des entités mentales et donc subjectives, mais comme des entités objectives qui peuvent être un patrimoine commun à plusieurs individus. Dans La pensée (1918), Frege concevra l’objectivité des sens en termes explicitement platoniciens : « Un troisième règne sera reconnu », au-delà du règne des choses et de celui des représentations (1918 : 184) : c’est le règne des pensées, qui – comme les choses – ne sont pas de quelqu’un, et d’autre part ne sont pas perceptibles par les sens, comme ne le sont pas les représentations.

Frege semble souvent identifier le contenu objectif d’un énoncé – la pensée qu’il exprime – avec ses conditions de vérité : le sens d’un énoncé, dit-il par exemple, est « la pensée que [ses] conditions [de vérité] sont satisfaites » (1893 : § 32). Toutefois, sur ce point, sa position n’est pas univoque. Il semble quelquefois admettre que deux énoncés peuvent avoir les mêmes conditions de vérité, mais un sens différent (Casalegno, 1992 : 25-27). C’est dans le Tractatus de Wittgenstein (§ 11) que l’on trouvera pour la première fois une identification explicite et inconditionnée du sens d’un énoncé avec ses conditions de vérité. Il faut toutefois observer que la manière dont Frege justifie l’objectivité des pensées – qui, à ses yeux, en constitue la caractéristique essentielle – présuppose l’identification de sens et conditions de vérité. Une telle justification dépend, en fait, de ce que nous appelons aujourd’hui une conception réaliste de la vérité, c’est-à-dire de l’idée qu’un énoncé est vrai ou faux en fonction de l’état réel des choses, indépendamment du fait que nous sachions quel est cet état, que nous puissions le savoir, et indépendamment même de notre propre existence. « La pensée que nous articulons dans le théorème de Pythagore est vraie intemporellement, vraie indépendamment du fait que quelqu’un puisse la considérer comme vraie [...] Elle est vraie non seulement à partir du moment où le théorème a été découvert – tout comme une planète est dans un rapport d’action réciproque avec d’autres planètes avant même qu’elle soit découverte » (Frege, 1918 : 184). Par conséquent, les conditions de vérité d’un énoncé sont indépendantes du fait qu’il soit formulé, compris, etc. ; et c’est en cela que consiste, pour Frege, l’objectivité de la pensée que l’énoncé exprime. Donc l’objectivité des pensées n’est pas autre chose que l’objectivité des conditions de vérité des énoncés.

Fidèle à une tradition qui a de lointaines origines, Frege distingue entre saisir une pensée et juger qu’elle est vraie. La pensée exprimée par un énoncé – la pensée que “Cesenatico est en Italie” par exemple – peut être conçue sans être nécessairement assertée : cette même pensée est également exprimée par la question “Cesenatico est en Italie ?”, dans laquelle pourtant elle n’est pas assertée. Les deux énoncés, l’assertion et la question, se distinguent du point de vue de leur force : assertorique dans le premier cas, interrogative dans le second. On trouve donc chez Frege un embryon de théorie des actes de langage, qui sera amplement développée par la suite (§ 25).

7. Limites de la compositionnalité

La valeur sémantique du tout n’est pas toujours fonction des valeurs sémantiques des parties : c’est du moins ce qu’il semble à première vue. C’est le cas des contextes énonciatifs que Frege appelle indirects, tels que (3) :

(3) Copernic croyait que les orbites des planètes étaient des cercles.

(3) contient, comme son constituant, l’énoncé (4)

(4) Les orbites des planètes sont des cercles.

Or, (4) est faux (dénote le Faux) ; toutefois, si nous le remplaçons – dans le contexte de (3) – par un autre énoncé également faux, et donc de dénotation identique, nous n’obtenons pas nécessairement un énoncé ayant la même valeur de vérité que (3). Par exemple, en remplaçant (4) par “La Lune est un fromage”, nous obtenons

(5) Copernic croyait que la Lune était un fromage

ce qui est faux, alors que (3) est vrai.

Ces exceptions à la compositionnalité auraient pu inciter Frege à revoir ses idées sur le sens et la dénotation des énoncés. Au contraire, il ne consent à les corriger que dans le cas particulier des contextes indirects. Dans un contexte tel que (3), un sous-énoncé tel que (4), selon Frege (1892b : 112), ne dénote pas sa dénotation habituelle (c’est-à-dire une valeur de vérité), mais dénote une pensée, et précisément la pensée qu’il exprime normalement, à savoir son sens habituel. Les mots “que les orbites des planètes étaient des cercles” dénotent le sens de l’énoncé (4).

Si nous admettons cela, le principe de compositionnalité est sauf, même dans le cas des contextes indirects : en effet, si, dans ces contextes, nous remplaçons un sous-énoncé par un autre de même sens (c’est-à-dire la même « dénotation indirecte »), la valeur de vérité de l’énoncé tout entier ne change pas. Le prix à payer pour sauver la compositionnalité est pourtant très élevé : les mêmes mots se trouvent avoir des dénotations différentes dans des contextes différents. En outre, le caractère nébuleux des indications de Frege à propos des conditions d’identité du sens (quand deux expressions différentes ont-elles le même sens ?) rend sa proposition difficile à vérifier. On comprend donc pourquoi la recherche sémantique qui a suivi n’a pu se satisfaire de cette solution de Frege, et a cherché d’autres voies (qui n’en seront pas plus heureuses, comme nous le verrons aux § 15, 33).

8. Prédicats et concepts

Dans l’essai Fonction et concept, Frege essaye d’éclaircir la notion mathématique de fonction, et montre qu’elle est d’une application plus générale que ne l’admettent ordinairement les mathématiciens. On dit habituellement que

(6) 2 · x³ + x

est « fonction de x », ou que

(7) 2 · 2³ + 2

est « fonction de 2 ». Mais l’expression (7) ne désigne nullement une fonction : elle est un symbole complexe qui dénote un nombre (le nombre 18). Si (7) était l’expression d’une fonction, les fonctions ne seraient rien d’autre que des nombres. Du reste, (6) désigne également un nombre, fût-ce de manière indéterminée : (6) désigne la valeur de la fonction pour l’argument x. L’« essence » de la fonction est dans la forme commune à (6) et (7) (et à un nombre infini d’autres expressions : 2 · 1³ + 1, 2 · 3³ + 3, etc.) que nous pourrions représenter par

(8) 2 · ()³ + ()

Comme on le voit en (8), une fonction est essentiellement incomplète ; ce que l’on obtient en complétant la fonction est sa valeur pour un argument déterminé. Nous appelons parcours de valeurs d’une fonction l’ensemble de ses valeurs pour ses arguments. Dans le cas de (8), le parcours des valeurs est {3, 18, 57, ...}. Deux fonctions distinctes comme x² – 4x et x(x – 4) peuvent avoir le même parcours de valeurs (1891 : 90).

Les fonctions n’ont pas toutes pour valeur des nombres : il y a des fonctions dont la valeur est une valeur de vérité (le Vrai ou le Faux). C’est le cas, par exemple pour la fonction x² = 1 : sa valeur pour x = –1 est le Vrai, pour x = 0 est le Faux, etc. On peut exprimer cela en disant que « – 1 a la propriété d’avoir 1 comme sa valeur au carré » ou encore que « – 1 relève du concept racine carrée de 1 ». « Nous voyons ainsi – dit Frege – à quel point ce qu’en logique nous nommons “concept” est intimement lié à ce que nous appelons “fonction”. Et on pourrait même dire qu’un concept est une fonction dont la valeur est toujours une valeur de vérité » (1891 : 99, c’est Frege qui souligne).

Le concept – qui est une fonction, et donc quelque chose d’incomplet, ou comme dit Frege de non saturé – ne doit pas être confondu avec son extension, qui est le parcours des valeurs de la fonction, à savoir un objet du type {Vrai, Faux, Faux, Vrai,...}, et donc quelque chose de complet.

Le langage naturel est capable lui aussi d’exprimer des fonctions. Par exemple, on peut considérer que l’expression “la capitale de __” désigne une fonction, qui fait correspondre à chaque pays sa capitale (son parcours de valeurs est l’ensemble des capitales). Et le langage naturel est en particulier capable d’exprimer des concepts, c’est-à-dire des fonctions dont la valeur est une valeur de vérité. Par exemple, l’expression “__ est la capitale de la France” dénote une fonction qui assume la valeur Vrai pour l’argument Paris, et Faux pour tous les autres arguments. De la même manière, “__ est un homme” dénote une fonction qui assume la valeur Vrai si l’argument est un homme et Faux dans tous les autres cas (par exemple la valeur Vrai, si elle est appliquée à Frege, et la valeur Faux si elle est appliquée à Paris).

Les expressions telles que “__ est un homme” sont appelées normalement des prédicats. Les prédicats sont donc des expressions linguistiques qui dénotent un type particulier de fonctions : des fonctions dont les valeurs sont des valeurs de vérité, c’est-à-dire des concepts.

Sur cette base, Frege analyse les énoncés simples, que Wittgenstein et Russell nommeront, par la suite, « atomiques » : des énoncés tels que “Socrate est un homme”. Pour Frege également, comme pour l’analyse traditionnelle, cet énoncé est constitué de deux « segments » : “Socrate” et “__ est un homme”. “Socrate” est un nom propre et a – comme nous le savons – un sens et une dénotation. Le prédicat “__ est un homme” dénote le concept homme, c’est-à-dire une fonction qui assigne à un argument le Vrai si l’argument est un homme, et le Faux dans tous les autres cas. Il y a donc une certaine asymétrie entre le traitement du sujet et le traitement du prédicat : “Socrate” dénote directement un objet (à savoir Socrate), tandis que “__ est un homme” dénote un concept, qui, à son tour, a une certaine extension. Comme on le verra (§ 14), dans les années quarante, cette analyse sera fortement simplifiée, et l’on dira que les prédicats dénotent simplement des classes (“__ est un homme” dénote la classe des hommes). Mais pour Frege, il est crucial qu’il n’en soit pas ainsi : les prédicats doivent dénoter des fonctions, c’est-à-dire des entités non saturées. Ce n’est que de cette manière que l’on peut expliquer le « lien propositionnel », ce qui « maintient » une proposition : une proposition s’obtient en « saturant » un concept avec un objet. Le concept a ce qu’on appellerait des « valences libres » : ces valences sont saturées par les objets. Si nous disions que le prédicat “__ est un homme” ne dénote pas un concept, mais directement la classe des hommes, nous ne serions plus en mesure, dit Frege, d’expliquer le lien propositionnel. Une classe est un objet comme un autre, elle n’est nullement incomplète. C’est pourquoi l’analyse « asymétrique » est la seule correcte : elle est la seule qui puisse rendre compte de l’unité de la proposition.

9. Russell : forme grammaticale et forme logique.

Le philosophe et mathématicien anglais Bertrand Russell (1872-1970), auteur des Principes de la mathématique (1903), était un grand admirateur de l’œuvre de Frege (il contribua à lui donner une audience internationale), et s’accordait avec lui sur l’idée d’une réductibilité de la mathématique à la logique. Toutefois, dans l’article Sur la dénotation (1905), Russell attaqua le cadre conceptuel frégéen de Sens et dénotation, en lui opposant une analyse du langage qui se dispensait du concept de sens : la seule propriété sémantique d’une expression linguistique qui soit de quelque importance pour la valeur de vérité des énoncés dans lesquels elle apparaît, c’est sa dénotation. Cette position est, à première vue, absolument contraire à l’intuition : comment expliquer par exemple la différente valeur de vérité de

(9) George IV voulait savoir si Scott était l’auteur de Waverley

(dont nous pouvons supposer qu’elle est vraie) et

(10) George IV voulait savoir si Scott était Scott

(probablement fausse), étant donné que Scott est l’auteur de Waverley, et que les deux expressions “Scott” et “l’auteur de Waverley” ont pourtant la même dénotation ? Le fait est, d’après Russell, que (malgré les apparences) l’énoncé (9) ne contient nullement comme constituant “l’auteur de Waverley”. En réfléchissant sur les énoncés qui contiennent des descriptions, indéfinies (“un homme”) ou définies (“l’auteur de Waverley”, “l’actuel roi de France”), Russell se convainc que la forme grammaticale superficielle de ces énoncés masque leur véritable forme logique, c’est-à-dire leur structure sémantique effective. La forme logique des énoncés contenant des descriptions indéfinies est reconduite par Russell à la quantification existentielle : par exemple, “J’ai rencontré un homme” peut être paraphrasé sous la forme “Il existe (au moins) un x tel que x est un homme et j’ai rencontré x”. Dans la paraphrase, qui exprime de manière transparente la forme logique de l’énoncé, l’expression “un homme” n’apparaît plus comme constituant. De la même manière, “L’actuel roi de France est chauve” – qui semble contenir un constituant dépourvu de dénotation, la description définie “l’actuel roi de France” – « dit » en réalité : il existe un x qui est actuellement roi de France ; il n’y a qu’un seul x qui soit tel ; et x est chauve (dans un langage de premier ordre avec identité , ($x) ((Rx & ("y)(Ry … y = x)) & Cx)). Il s’agit donc d’un énoncé faux, et non d’un énoncé dépourvu de valeur de vérité comme le pensait Frege (§ 5) : des expressions telles que “l’actuel roi de France” ou ”la montagne d’or” ne nous obligent nullement à postuler des entités inexistantes (comme Russell lui-même l’avait soutenu dans les Principes de la mathématique) ni à violer le principe du tiers exclu (la position de Frege selon Russell).

À travers la paraphrase proposée par Russell, l’énoncé “L’actuel roi de France est chauve” est réduit à une formulation où apparaissent seulement des expressions (prédicats) qui dénotent des propriétés des individus, outre l’apparat de la quantification (« il existe », « pour chaque... »). Pourraient y figurer également des noms propres, c’est-à-dire des expressions qui ne dénotent pas des propriétés mais des individus. Mais, dans ce cas également, il n’est pas sûr que les expressions dont l’apparence grammaticale est celle des noms propres (“Socrate”, “Pégase”) soient tels véritablement, à savoir des noms logiquement propres (comme le dira Russell par la suite, 1918-1919 : 359). « Un nom, au sens logiquement restreint de “mot dont la signification est un individu”, ne peut être appliqué qu’à un individu dont le locuteur a une connaissance directe (acquaintance) » (Ibidem). Le concept de nom propre, pour Russell, est donc un concept sémantique (celui d’une expression qui dénote un individu) qui est fondée épistémologiquement sur la distinction entre connaissance directe et connaissance « par description ». « Chaque pensée – dit Russell – doit partir de la connaissance directe [par exemple celle que j’ai de la surface de la mer que je vois de ma fenêtre], mais il est possible de penser à de nombreuses choses dont on n’a pas de connaissance directe » (1905 : 204). De nombreuses choses ne sont connues qu’à travers leurs propriétés, c’est-à-dire à travers une description que l’on peut avoir d’elles : ainsi, nous ne connaissons pas Socrate directement, mais comme tel philosophe athénien, maître de Platon, etc. Plus tard, Russell dira que la plus grande partie des noms propres grammaticaux sont en réalité des abréviations de descriptions ; et de plus ce qui est décrit n’est pas un individu (particular) véritable, mais un « système compliqué de classes et de séries » (1918-1919 : 359).

Comment décider si une expression est véritablement un nom propre ou au contraire une description « déguisée » ? Comment décider, en fait, quelle est la véritable forme logique d’un énoncé du langage ? Il est clair qu’en prenant une telle décision, nous ne sommes pas guidés uniquement par des intuitions linguistiques, mais aussi et surtout par notre jugement épistémologique et par nos opinions ontologiques (cf. Di Francesco, 1990 : 42-43). La distinction entre nom propre au sens grammatical et au sens logique est un formidable principe de manipulation du langage sur des présupposés ontologiques. Russell en était conscient à sa manière, quand il soutenait qu’un « solide sens de la réalité » était indispensable pour une analyse correcte du langage, parce que la « logique, pas plus que la zoologie, ne peut admettre l’existence d’une licorne » (1919 : 202). L’analyse des énoncés sur le type de celui sur le roi de France est également guidée à la fois par des intuitions sémantiques (sur ce que « l’on veut dire » avec de tels énoncés) et des présupposés ontologiques (quels types d’entités peut-on admettre dans une ontologie « saine »).

La conception purement dénotative du langage de Russell (reprise plusieurs dizaines d’années plus tard par les théoriciens de la référence directe, § 32) contribuera à la longue éclipse de la notion frégéenne de sens. Elle eut une forte influence sur la formation du Tractatus logico-philosophicus de Wittgenstein pour au moins trois aspects : la distinction entre forme grammaticale et forme logique, l’idée d’analyse – l’opération qui récupère la forme logique au-delà de l’apparence grammaticale – et l’idée que la proposition « analysée » (c’est-à-dire considérée sous sa forme logique) est essentiellement une connexion de noms qui dénotent directement des individus ou des propriétés.

10. Le Tractatus logico-philosophicus : théorie de l’image.

Les réflexions sur le langage du jeune philosophe autrichien Ludwig Wittgenstein (1889-1951), élève de Russell à Cambridge, et bon connaisseur des œuvres de Frege, sont synthétisées dans un petit livre de quelques quatre-vingt pages, le Tractatus logico-philosophicus (1922). Le but principal du Tractatus est de répondre à la question : en quoi les propositions de la logique se distinguent-elles de toutes les autres propositions du langage ? Pour répondre à cette question, Wittgenstein formule une théorie générale du langage, dans laquelle il s’agit de saisir « l’essence de la proposition » (1914-1916 : 22.1.1915), c’est-à-dire des énoncés déclaratifs. Il est d’accord avec Russell sur la conception d’une proposition simple telle qu’une structure relationnelle (de type Rabc), qui asserte que certains objets (a, b, c) ont entre eux une relation R : par exemple que a se trouve entre b et c. Mais une proposition a aussi une forme (par exemple, la forme de Rabc pourrait être indiquée par “Xxyz”) ; et Russell, à cette époque, avait tendance à concevoir les formes propositionnelles comme des « objets logiques » simples, dont la connaissance directe (acquaintance) est présupposée par la compréhension du langage. Mais – objectait Wittgenstein – si les formes sont des objets logiques, de quelle manière une proposition peut-elle nous communiquer sa forme ? Certainement pas en la désignant par un nom, parce que cela ne ferait qu’ajouter un constituant à la proposition, en en modifiant la forme ; mais pas même en l’exprimant par une proposition, parce que cela impliquerait une régression à l’infini (1914-1916 : 20.11.14). La forme doit être exhibée par la proposition : de même qu’une photographie exhibe la structure de la situation qu’elle représente (elle fait voir, à travers la disposition de ses éléments, que les choses se présentent de telle ou telle manière dans la réalité), une proposition montre la structure de ce qu’elle asserte. Comme dans le cas de la photographie, la structure qu’elle exhibe est la structure de ce dont on asserte la subsistance (c’est-à-dire de l’état des choses dont on asserte qu’il est un fait : la proposition « le chat est sur la table » asserte que c’est un fait que le chat est sur la table).

Wittgenstein en arrive donc à penser une proposition comme une image (Bild). Ce n’est qu’en concevant la proposition comme une image que nous parvenons à rendre compte du fait qu’elle peut nous communiquer une information nouvelle. Elle nous dit quelque chose de la réalité, que nous ne savions pas auparavant ; et elle nous le dit en utilisant uniquement ses parties constituantes – les mots – et leur disposition. « Une proposition doit communiquer avec des expressions anciennes un sens nouveau. La proposition nous communique une situation ; elle doit donc avoir une interindépendance essentielle avec cette situation. Et cette interdépendance consiste justement en ce qu’elle est l’image logique de la situation » (1922 : 4.03). Wittgenstein nous invite à accomplir un processus d’abstraction, à partir des images au sens ordinaire du terme jusqu’à la proposition comme image logique ; et il essaie de nous faire voir que, dans ce processus, « l’essentiel de la représentation par l’image » (4.016) n’est pas perdu. Une photographie en noir et blanc, par exemple, « ressemble » intuitivement à la situation qu’elle représente ; mais, à y regarder de plus près, dans la photo il n’y a pas de tridimensionnalité, les relations chromatiques entre les objets réels sont représentées par des relations du type « plus clair » ou « plus foncé » et les dimensions des objets représentés sont différentes de celles des parties correspondantes de la photo (même si les proportions sont conservées). La photographie représente la réalité avec ses moyens, sur la base de certains conventions, du point de vue d’une certaine forme de la représentation. Dans un dessin stylisé,

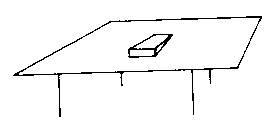
la « ressemblance » (l’iconicité) est confiée uniquement au maintien de certaines relations géométriques et métriques : l’image de l’album est sur l’image de la table et en contact avec l’image du plan de table, l’image des pieds forme un angle droit avec l’image du plan (comme dans la réalité), etc. La forme de la représentation est changée : le dessin n’est plus en mesure de représenter des relations chromatiques (comme c’était le cas de la photographie), mais peut encore représenter des relations géométriques. Le plus haut niveau d’abstraction est atteint par une forme de représentation qui rend compte des relations en général (non pas des relations spatiales avec des relations spatiales, etc.) : c’est la forme logique, et une image qui aurait comme forme de représentation la forme logique est dite image logique (1922 : 2.181). Chaque image est aussi logique (2.182), parce que chaque image résulte d’éléments qui ont telle ou telle relation ; la forme logique – le fait de pouvoir être représenté à travers des relations entre éléments, et donc d’avoir une structure – c’est « la forme de la réalité » (2.18), mais l’image seulement logique des faits, c’est la pensée (3.). La pensée est le système de représentation dans lequel les images n’ont en commun avec les faits représentés que la structure au sens le plus abstrait du terme (et non la structure spatiale ou chromatique, etc.).

Le langage est l’expression sensible de la pensée (3.1) ; dire « pensée » (dans le sens d’« une pensée ») revient à dire « proposition dotée de sens » (4.). Mais la proposition coïncide avec la pensée – et est donc une image logique – à deux conditions : (a) si elle est entendue non pas comme simple signe, configuration d’encre sur du papier (ou de phonèmes, etc.), mais comme signe pensé (3.5), c’est-à-dire mis en relation avec la réalité ; (b) si elle est considérée comme complètement analysée (3.2-3.201), c’est-à-dire une fois qu’ont été « démontées » les conventions linguistiques spécifiques à travers lesquelles « le langage travestit les pensées » (4.002). Mais de quelle manière une proposition, qui se présente comme une liste de mots, peut-elle être une image, c’est-à-dire un fait structuré (comme une photographie ou un dessin) qui représente un autre fait ? qu’est-ce qui « maintient » une proposition, en en faisant un tout articulé ? Comme on l’a vu, Frege avait reconduit la connexion de la proposition à la combinaison d’entités saturées (objets) et non saturées (concepts). Wittgenstein au contraire, conçoit la proposition comme un enchaînement de noms ou de signes simples (4.22) qui signifient (tiennent lieu) des objets du monde. Les objets, comme les noms, sont tous non saturés : ils sont essentiellement des entités combinables, non pas sans discrimination mais à certaines conditions. La nature non saturée des noms est le fondement de l’adhésion du Tractatus au principe de la contextualité de Frege : « Ce n’est que dans le contexte de la proposition qu’un nom a une signification » (3.3), parce que la signification d’un nom – l’objet qu’il dénote – se donne seulement en configurations, en combinaisons avec d’autres objets (Wittgenstein nomme ces configurations états de choses), représentées par des propositions. On voit ainsi que la philosophie du langage du Tractatus ne peut être caractérisée comme atomisme logique que dans une certaine mesure seulement. Il est certain que Wittgenstein admet des « atomes », termes ultimes de l’analyse : ce sont justement les objets. Afin que le sens d’une proposition soit déterminé, il faut que son analyse prenne fin, et de fait, il doit y avoir des objets simples qui en constituent le point d’arrivée. Sans quoi, « il en résulterait que pour une proposition, avoir un sens dépendrait de la vérité d’une autre proposition » (2.0211) : pour être sûrs qu’une proposition parle de quelque chose (et non de rien) et donc ait un sens, nous devrions être garantis (par une autre proposition) que les objets dont la première parle subsistent effectivement. Mais les objets du Tractatus ne sont pas comme les particulars de l’atomisme logique de Russell (1918-1919 : 360), complètement indépendants logiquement les uns des autres : chaque objet est logiquement lié – par sa forme – aux objets avec lesquels il peut se combiner, et négativement, à ceux avec lesquels il ne peut pas se combiner. Pour Wittgenstein (1922 : 1.21, 2.061, etc.), ce sont les états de choses, et non les objets, qui jouissent de l’indépendance absolue réciproque dont parle Russell ; et cette indépendance s’étend aux propositions qui les représentent (5.134, 6.3751).

Pour Wittgenstein, comme pour Frege, les propositions ont un sens (les noms, au contraire, n’ont pas de sens : leur valeur sémantique est simplement leur dénotation). Le sens d’une proposition est ce que l’on connaît quand on comprend la proposition, donc (la proposition étant une image) l’état de choses figuré, à savoir la manière dont les choses sont si la proposition est vraie. La proposition montre comment sont les choses (montre son sens) et dit que les choses sont ainsi (4.022). Elle peut être vraie (si les choses sont effectivement ainsi) ou fausse (si les choses ne sont pas ainsi) ; pour savoir si la proposition est vraie, il faut la confronter à la réalité. Mais pour la comprendre il n’est pas nécessaire de savoir qu’elle est vraie ou qu’elle est fausse ; la comprendre, c’est « savoir ce qu’il advient si elle est vraie » (4.024). De cette manière Wittgenstein institue le rapport entre signification énonciative et vérité, qui sera centrale dans le paradigme dominant.

Que seuls les énoncés factuels sont sensés est un corollaire de cette définition du sens ; restent en dehors du langage les énoncés évaluatifs (comme par exemple ceux de l’éthique et de l’esthétique), et ceux qui, au lieu de représenter des faits, tentent de représenter les traits généraux du langage et du monde : et donc les propositions de la métaphysique, et même celles dont se compose le Tractatus. Elles sont des « tentatives de dire ce qui peut seulement se montrer » (Kenny, 1973 : 124). On peut soutenir, toujours avec Kenny (Ibidem), et finalement avec Wittgenstein lui-même (1922 : 6.54) qu’« elles ne sont pas pour autant inutiles : précisément leur faillite et les modalités de leur insuccès sont instructives ».

11. Sens et conditions de vérité

Les propositions les plus simples, que Wittgenstein appelle propositions élémentaires, ont les caractéristiques décrites jusqu’à présent : ce sont des connexions de noms, qui constituent des images des états de choses. « Un nom est pour une chose, un autre pour une autre chose et ils sont liés entre eux : ainsi le tout représente – comme un cadre plastique – l’état des choses » (4.0311). Mais dans le langage, il y a aussi des propositions complexes : par exemple les négations, les conjonctions, les disjonctions, etc. Ces propositions contiennent des expressions – les « constantes logiques » comme “ne pas” “et”, “ou”, etc. – qui, selon Russell, signifiaient des « objets logiques ». Pour Wittgenstein, au contraire, les constantes logiques n’ont pas de valeur désignative : il n’y a rien, au monde, qui corresponde au signe de négation ou de conjonction (4.0312). Les constantes logiques ont pour seule fonction de déterminer de quelle manière le sens d’une proposition complexe où elles apparaissent, dépend du sens des propositions plus simples dont elle est constituée. Le sens de chaque proposition complexe, en effet, dépend (pour Wittgenstein comme pour Frege) du sens des propositions élémentaires dont elle est constituée (cf. 5.2341). Dans le Tractatus, le principe de compositionnalité s’avère être une conséquence de la définition du sens de la proposition. Une proposition est sensée si et seulement si elle montre de quels états de choses elle affirme la subsistance ou la non-subsistance. Donc, pour qu’une proposition soit sensée, il faut que l’on voit, à partir de la proposition elle-même, quels états de choses subsistent (ou ne subsistent pas) si la proposition est vraie ; c’est-à-dire quelles propositions élémentaires sont vraies (ou fausses) si la proposition est vraie. Par exemple, la proposition « A est rouge et B est jaune » montre qu’elle affirme la subsistance de deux états de choses, que A est rouge et que B est jaune ; ou, en d’autres termes, elle montre qu’elle est vraie si (et seulement si) les deux propositions « A est rouge » et « B est jaune » sont également vraies. Le sens de la proposition tout entière (sa possibilité de vérité) dépend des sens des propositions constituantes (de leur possibilité de vérité). Si nous avons affaire à une proposition sensée, nous devons être en mesure de calculer pour quelles valeurs de vérité des constituants élémentaires la proposition est vraie et pour lesquelles elle est fausse. « La proposition est une fonction de vérité des propositions élémentaires » (1922 : 5.). En principe, toute proposition sensée doit présenter (a) les propositions élémentaires dont dépend sa valeur de vérité, et (b) comment elle en dépend. De fait, les deux aspects peuvent être plus ou moins « masqués » par la forme grammaticale superficielle de la proposition ; c’est alors à l’analyse logique de reconstruire la proposition de manière à ce que l’on voit que sa valeur de vérité dépend des valeurs de vérité des propositions élémentaires dont elle est constituée. Wittgenstein accepte donc l’idée russellienne d’analyse, et la distinction entre forme grammaticale et forme logique sur laquelle elle est fondée.

Le Tractatus nomme les possibilités de vérité des constituants élémentaires : « conditions de vérité » de la proposition (4.41, 4.431) ; et soutient que la proposition « est l’expression de ses conditions de vérité » (4.431). Cette affirmation a un sens précis : Wittgenstein pense que, au lieu de “p et q”, nous pourrions écrire :

« p q

V V V

V F F

F V F

F F F »

(cf. 4.442). Cette table pourrait être lue : « La proposition qui est vraie si p et q sont toutes deux vraies, fausse si p est vraie et q est fausse, fausse si p est fausse et q est vraie, fausse si p et q sont toutes deux fausses », ou tout simplement « la proposition qui est vraie si et seulement si p et q sont vraies ». De cette manière, il deviendrait évident que ce que la proposition exprime est une dépendance déterminée des valeurs de vérité possibles de ses constituants élémentaires. Et puisque ce qu’une proposition exprime, c’est son sens, il est correct de dire que le sens d’une proposition ce sont ses conditions de vérité.

« Parmi les groupes possibles de conditions de vérité, il y a deux cas extrêmes » (4.46) : celui d’une proposition vraie pour n’importe quelle combinaison de valeurs de vérité de ses constituants élémentaires et celui d’une proposition fausse pour n’importe quelle combinaison. Le premier cas c’est la tautologie. Le second, la contradiction. Sont tautologiques, par exemple, des énoncés tels que “Si Bachibouzouque est une expression du Capitaine Haddock, alors Bachibouzouque est une expression du Capitaine Haddock”, ou “Soit il neige, soit il ne neige pas” ; “Il pleut et il ne pleut pas”, par contre, est une contradiction. Les propositions de la logique (au sens de Wittgenstein) s’avèrent être des tautologies. Il faut ici se souvenir qu’à l’époque de la composition du Tractatus, les relations entre la partie propositionnelle et la partie prédicative de la logique élémentaire étaient encore peu connues. En particulier, l’inexistence d’un processus mécanique de décision pour la logique des prédicats de premier ordre ne sera démontrée (par Church) qu’en 1936 ; c’est pourquoi Wittgenstein pouvait écrire – par exemple – que « la démonstration dans la logique n’est qu’un moyen mécanique pour reconnaître plus facilement la tautologie lorsque celle-ci est compliquée » (1922 : 6.1262). Il ne voyait pas de grandes différences entre logique propositionnelle (théorie des fonctions de vérité) et logique prédicative (théorie de la quantification), et considérait la tautologie comme l’essence de la vérité logique en général ; alors qu’en réalité, seul un sous-ensemble des théorèmes de la logique prédicative peut être considéré comme des tautologies au sens de Wittgenstein.

Les propositions de la logique, donc, se distinguent de toutes les autres parce qu’elles sont vraies quel que soit l’état des choses : leur vérité est indépendante des faits du monde, et donc elle peut être déterminée sans que celles-ci soient confrontées au monde (6.113), contrairement à ce qui se passe avec les autres propositions. Elles n’ont aucun contenu représentationnel : « Ce ne sont pas des images de la réalité » (4.462), elles ne « traitent » de rien (6.124), ne disent rien (6.11). Une tautologie ne fait pas autre chose qu’exhiber les propriétés du langage : « Que ses parties constitutives, reliées de la sorte, produisent une tautologie, caractérise la logique de ses parties constitutives » (6.12). Qu’une proposition soit une tautologie, selon Wittgenstein, cela se voit (6.127) : tenter de le dire – tenter de représenter le fait qu’une certaine proposition est une tautologie – nécessiterait que soit représentée la forme d’une proposition (qui est en effet une tautologie en vertu de sa forme). Mais c’est impossible, d’après Wittgenstein, parce que nous ne pouvons pas « sortir » de notre système de représentation (c’est-à-dire de notre langage) pour en représenter les propriétés. Figurer les conditions de la représentation reviendrait à les traiter comme des situations, dont on affirme la subsistance. Mais si l’on peut affirmer qu’une situation subsiste, il doit être possible également d’affirmer qu’elle ne subsiste pas : il doit être possible, donc, de dire comment seraient les choses si les conditions de la représentation n’étaient pas données, ce qui est absurde.

En général, les propriétés d’un symbolisme se voient à partir du symbolisme lui-même. Des formulations « métalinguistiques » comme « “P” est un prédicat », « “x” est une variable individuelle », etc., sont dénuées de sens pour Wittgenstein. Mais plus encore : m&Mac253 ;me dme des formulations à première vue non métalinguistiques, comme les énoncés d’identité (“a = b”, “a = a”), sont, sinon dénuées de sens, en tout cas hors de propos : dans un symbolisme adéquat, que deux objets soient distincts devrait être exprimé par le fait qu’ils ont deux noms différents (et réciproquement, à des noms différents devraient correspondre des objets différents), tandis qu’avoir affaire à un seul objet devrait être exprimé par le fait que l’on dispose d’un seul nom (5.53). Les expressions de forme “a = b” sont tout au plus « des auxiliaires de la figuration » (4.242) : ils expriment qu’un certain objet a deux noms (le symbolisme est donc imparfait). Cette position drastique de Wittgenstein sur le symbolisme doit être rapprochée du fait que pour le Tractatus, il n’y a qu’un seul langage (le langage), et il n’existe donc pas un autre langage qui en décrirait les propriétés.

12. Le néo-positivisme et l’interprétation empiriste du Tractatus.

Les philosophes néo-positivistes du « Cercle de Vienne » (parmi lesquels M. Schlick, R. Carnap, O. Neurath) lurent avec attention le Tractatus logico-philosophicus. Certains n’en apprécièrent pas la dernière partie (sur l’éthique et le mystique), mais tous s’accordèrent, en substance, sur la philosophie du langage et la logique. Toutefois, les néo-positivistes ne purent souscrire aux thèses du Tractatus que « dans la mesure où il[s] pouvai[en]t les assimiler à [leur] conception de fond » (Carnap, 1963 : 24) ; c’est-à-dire au prix d’un certain malentendu, qui devint évident quand Wittgenstein rencontra personnellement Schlick, Carnap et d’autres membres du Cercle de Vienne dans les années 1929-1932. Les néo-positivistes pensaient, tout d’abord, que le langage qu’évoquait le Tractatus était un langage idéal : convaincus qu’ils étaient de la supériorité absolue des langages artificiels symboliques sur les langues naturelles, ils donnaient pour acquis que les propriétés que Wittgenstein attribuait au langage, avec sa théorie de la figurtation et de la véri-fonctionnalité, ne pouvaient concerner le langage naturel. En outre, les néo-positivistes tendaient à faire une lecture empiriste du Tractatus, en interprétant la réduction de toutes les propositions à des fonctions de vérité de propositions élémentaires comme une fondation de l’édifice de la science sur la base d’énoncés d’expérience. Carnap ne pensait pas être en désaccord avec Wittgenstein quand il écrivait que « chaque énoncé de la science est, en dernière analyse, un énoncé sur les relations qui subsistent entre les expériences élémentaires [Elementarerlebnisse], de sorte que toute connaissance qui a un contenu (qui ne soit pas purement formel) se reconduit à l’expérience » (Carnap, 1928 : § 183). Par conséquent, la proposition 4.024 du Tractatus (« Comprendre une proposition, c’est savoir ce qu’il advient si elle est vraie » cf. § 10) est interprétée comme si l’on affirmait qu’un énoncé est compris si l’on est en mesure d’en déterminer la vérité ou la fausseté par rapport à l’expérience, c’est-à-dire de le vérifier empiriquement : « “vérification” signifie : contrôle par rapport aux expériences » (Carnap, 1928 : § 179). La vérifiabilité empirique est donc, pour les néo-positivistes, un critère de signification : « Établir la signification d’un énoncé équivaut à établir les règles selon lesquelles l’énoncé est utilisé, ce qui, à son tour, revient à établir la manière dont il peut être vérifié (ou falsifié). La signification d’un énoncé est la méthode de sa vérification » – comme l’écrit Schlick, en se référant explicitement à Wittgenstein (Schlick, 1936 : 458) – et si un énoncé n’est pas empiriquement vérifiable (et n’est pas même une vérité logique ou mathématique) il est dénué de sens. En réalité, la formulation du Tractatus était épistémologiquement neutre : elle établissait une identité entre compréhension de l’énoncé et connaissance de ses conditions de vérité, sans s’engager quant au lieu et au mode de l’établissement de sa vérité ou fausseté.

Les néo-positivistes utilisèrent le critère de la vérifiabilité empirique comme instrument de leur combat antimétaphysique. Pour eux, les énoncés de la métaphysique ne sont pas faux, mais bien au contraire dépourvus de sens (comme l’avait déjà dit Wittgenstein, 1922 : 4.003), soit parce qu’ils sont mal formés syntaxiquement, soit parce qu’ils utilisent des signes dépourvus de signification ; et un signe est dépourvu de signification si son critère d’application n’est pas spécifié, c’est-à-dire si ne sont pas spécifiées les conditions de vérité des propositions les plus simples dans lesquelles le signe apparaît, à savoir (en dernière analyse) si les propositions simples susdites ne sont pas logiquement équivalentes à des énoncés d’expérience immédiate (propositions protocolaires), lesquels à leur tour, sont intrinsèquement sensés. Carnap (1932) donne l’exemple d’un prédicat – “babique” – que quelqu’un proposerait d’introduire dans le langage, en soutenant que certaines choses sont babiques et d’autres pas, mais « qu’il n’existe pas de qualités empiriques caractéristiques de la babicité ». Un tel pseudo-mot, n’ayant pas de critère d’application, serait dépourvu de signification, et l’emploi n’en serait pas licite, même si on nous assurait qu’en l’employant on voulut signifier quelque chose. Si une proposition simple, de forme “a est babique”, n’implique pas de propositions protocolaires et n’est pas impliquée par elles, “babique” n’a pas de signification. La signification d’un mot est donc, pour Carnap, sa contribution aux conditions de vérification des énoncés dans lesquels il apparaît.

On voit ainsi comment le néo-positivisme, et en particulier la pensée du premier Carnap, représente, en philosophie du langage, le développement d’une interprétation empiriste de la Première thèse du paradigme dominant (§ 4), selon lequel le concept de conditions de vérité est remplacé par celui de conditions de vérification empirique. Cette doctrine sémantique, que l’on appelle habituellement vérificationnisme, trouve toujours moins d’adeptes à partir de la moitié des années cinquante (sous sa forme extrême, Carnap l’avait d’ailleurs abandonnée dès les années trente). Quine (§ 27) a souligné la faillite des tentatives de réduire toutes les assertions scientifiques à des combinaisons d’énoncés d’expérience ; plus généralement, on eut de plus en plus la conviction que les énoncés parfaitement sensés, pour lesquels il est difficile de penser sérieusement que l’on puisse disposer d’une « méthode de vérification », sont innombrables, depuis “Les positrons sont faits de quarks” à “Aristote aimait les oignons” (les exemples sont de Fodor, 1981 : 216). On peut toutefois trouver quelque affinité avec le vérificationnisme dans la philosophie du langage de Dummett (§ 23), et plus encore dans certaines tendances actuelles de la sémantique cognitive (§ 33).

13. Tarski : une méthode pour l’explicitation des conditions de vérité.

Dans le Tractatus de Wittgenstein, l’analyse des conditions de vérité des énoncés simples (les propositions élémentaires) ne s’articule pas en une véritable théorie, également parce que la proposition « complètement analysée », celle dont il serait évident qu’elle est « l’image d’un état de choses », est loin de la surface du langage. Les énoncés simples du langage naturel – “Socrate court”, “J’ai vu une magnifique rose rouge”, “Alfred pense souvent à sa promotion”, – ne se présentent pas comme des enchaînements de noms propres. A l’intérieur du cadre théorique du Tractatus, il est difficile d’imaginer une méthode générale de détermination des conditions de vérité des énoncés simples tels qu’ils se présentent. Quant aux énoncés complexes, ils sont analysés comme s’ils étaient tous réductibles à des combinaisons de fonctions de vérité énonciatives (négations, conjonctions, disjonctions, etc.) perturbant également, en ce cas, la « surface » du langage, tel qu’il se présente. C’est à Alfred Tarski (1902-1985) que revient le mérite historique d’avoir rendu possible l’extension de l’analyse aux énoncés quantifiés (“Tous les hommes sont mortels”, “Il n’existe pas de nombre plus grand que tout nombre pair”) quelle qu’en soit la complexité, et à avoir fourni une méthode de détermination des conditions de vérité des énoncés simples plus facilement applicable au langage naturel. Ces deux résultats sont, dans une certaine mesure, un corollaire de la théorie de la vérité de Tarski (Tarski, 1933).

La vérité, pour Tarski comme déjà pour Aristote, est une propriété des énoncés d’un langage. Mais en quoi cela consiste ? Plus précisément : quelles conditions devons-nous satisfaire, en définissant une propriété d’énoncés, pour pouvoir dire que ce que nous avons défini est la vérité (et non une autre propriété) ? Outre une condition d’adéquation formelle, selon laquelle la définition ne doit pas engendrer de contradictions, voici ce que Tarski propose comme condition d’adéquation matérielle d’une définition de vérité (c’est-à-dire comme condition dont nous pouvons dire, l’ayant satisfaite, que nous avons défini la vérité) : une définition de “vrai (pour le langage L)” est matériellement adéquate si et seulement si on peut en déduire tous les énoncés de forme

(T) N est vrai (en L) si et seulement si p,

où “N” est le nom d’un énoncé donné de L, et p sa traduction – que l’on suppose préétablie – dans le métalangage dans lequel la définition est formulée (et par rapport auquel L est le langage-objet). « Tous » les énoncés cela veut dire : un pour chaque énoncé du langage-objet L. Le schéma (T) saisit, selon Tarski, le noyau minimum de nos intuitions sur la vérité : quelles que soient nos idées philosophiques à ce propos, nous sommes tous d’accord sur le fait que, si (par exemple) l’énoncé “Platon était un élève de Socrate” est vrai, alors Platon était un élève de Socrate, et réciproquement si Platon était un élève de Socrate, alors l’énoncé “Platon était un élève de Socrate” est vrai. Tarski pensait que le schéma (T) expliquait la « conception classique » de la vérité (selon laquelle “vrai” est synonyme de “correspondant à la réalité”) (Tarski, 1956 : 160 q.) ; mais il est fort douteux que (T) soit lié à cette conception plus qu’à d’autres (cf. Marconi, 1984).

En général, il n’est pas banal de satisfaire la condition d’adéquation matérielle, c’est-à-dire de donner une définition du prédicat “vrai”, dont on puisse démontrer qu’il rende déductibles tous les biconditionnels de la forme (T). Tarski donna un exemple, en formulant une définition de la vérité pour un langage formel et en montrant qu’une telle définition était conforme à ses critères. Le langage en question est du type dit « de premier ordre » (pour des raisons sur lesquelles il n’est pas question de s’attarder ici). Nous décrirons en détail un langage de ce type (que nous appellerons “L¹”) parce qu’il nous arrivera souvent par la suite de faire référence à des langages de premier ordre. Le langage dont s’occupe Tarski est différent de celui que nous allons décrire, mais nous l’appellerons également “L¹” parce que la différence, pour les aspects qui nous intéressent ici, est inessentielle.

Le vocabulaire de L¹ inclut : (a) des constantes individuelles (c’est-à-dire des noms propres d’individus) : a, b, c, ... ; (b) des variables individuelles x, y, z,... (que l’on suppose ordonnées) ; (c) des constantes prédicatives, à 1 place, 2 places, ... n places d’argument : P¹, Q¹, ... P², Q², ..., etc. ; (d) des symboles de fonctions ou foncteurs, à 1, 2, ..., n places d’argument : f¹, g¹, ... f², g², ..., etc. ; (e) les cinq connecteurs énonciatifs : ~ (négation), & (conjonction), & (d (disjonction), … (conditionnel), (biconditionnel) ; (f) les deux quantificateurs : universel (« pour tout »), ", et existentiel (« pour quelque »), $ ; (g) les deux parenthèses. La grammaire de L¹ détermine les notions de terme et de formule (bien formée) comme suit :

(1) les constantes individuelles et les variables individuelles sont des termes ;

(2) si t₁, t₂, ..., t_n sont des termes et fⁿ est un foncteur à n places, alors fⁿ (t₁ t₂ ... t_n) est un terme ;

(3) rien d’autre n’est un terme ;

(4) si t₁, t₂, ..., t_n sont des termes et Pⁿ est une constante prédicative à n places, alors Pⁿ t₁ t₂ ... t_n est une formule (atomique) ;

(5) si A et B sont des formules, alors ~ A, ( A & B), (A & B) B),

---

A …A … B), (A B) sont des formules ;

(6) si A est une formule et x_i est l’i-ème variable individuelle (pour n’importe quel i) (" x_i)A et ($x_i)A sont des formules ;

(7) rien d’autre n’est une formule.

Sont des formules de L¹, par exemple, “P²ab”, “P³af²(bd)c”, “("x₂)P¹x₂”, “("x₃)(P¹x₃ … ($x₁)Q²x₁x₃)”, etc. Un tel langage a un fort pouvoir expressif (même si, selon certains, il ne nous permet pas de dire des choses du type : « Toutes les qualités de Socrate sont de bonnes qualités »), et il est structurellement assez proche du langage naturel au point de conférer aux résultats de Tarski une certaine utilité pour l’analyse de ce dernier (comme le précise Tarski lui-même, 1956 : 165, n. 2). Les formules que nous venons de citer, par exemple, pourraient être mises en correspondance (dans un sens qu’il serait trop long à expliciter ici, cf. § 29) avec des énoncés français tels que (dans l’ordre) : “Georges aime Marie”, “Georges préfère la fille de Marie et Jacques à Charlotte”, “Toutes les choses passent”, ”Tous les hommes ont au moins un ami”.

La démarche de Tarski pour définir le prédicat de vérité pour ce langage, est plutôt complexe (pour une exposition détaillée mais élémentaire voir Casalegno et Marconi, 1992 : 55-63). Il suffira de dire que Tarski (1) définit la notion auxiliaire de satisfaction ; (2) qu’il définit le prédicat de vérité pour L¹ sur la base de la satisfaction ; et (3) qu’il montre que cette définition implique tous les biconditionnels de la forme (T). La notion de satisfaction (et indirectement celle de vérité) est définie par Tarski comme relation entre formules et objets ou séquence d’objets. Intuitivement, par exemple, un couple d’objets (a, b) satisfait la formule “Pxy” si (et seulement si) a et b sont dans la relation dénotée par “P”. Le passage par la notion de satisfaction est imposé par la structure du langage. Considérons en effet une formule L¹ de la forme Pⁿt₁t₂... t_n, dans laquelle n’apparaissent que des termes fermés, c’est-à-dire sans variables. Si toutes les formules de L¹ étaient soit de cette forme, soit des combinaisons véri-fonctionnelles de formules de cette forme (comme par exemple “(Pa & Qb)”, “(Pa … (Raf¹c & Qb))”, etc.), on pourrait penser définir “vrai (en L1)” de cette manière. Soit I une fonction qui assigne à chaque constante individuelle un individu dans le domaine de l’interprétation (c’est-à-dire dans l’ensemble des objets dont le langage parle), à chaque constante prédicative à n places un ensemble de n-ples d’éléments du domaine, et à chaque foncteur une fonction définie sur le domaine. Une formule atomique Pⁿt₁t₂... t_n est vraie si et seulement si <I(t₁), I(t₂), ... I(t_n)> appartient à I(Pⁿ) ; une négation, ~ A est vraie si et seulement si A n’est pas vraie ; une conjonction (A & B) est vraie si et seulement si A et B sont vraies toutes les deux, et ainsi de suite pour tous les autres connectifs (reproduisant substantiellement les tables de vérité du Tractatus). Mais les formules de L¹ ne sont pas toutes des combinaisons véri-fonctionnelles de formules fermées (c’est-à-dire dépourvues de variables non quantifiées) : L¹ comprend également des formules ouvertes, comme “P¹x₁”, et des formules fermées comme “("x₂)P¹x₂”, qui ne sont pas pour autant des combinaisons de formules fermées (mais d’une formule ouverte – “P¹x₂” – et d’un quantificateur). Et nous voulons dire ce qu’est être vrai pour n’importe quelle formule de L¹ ; et nous voulons le dire de manière finie, c’est-à-dire en spécifiant, en un nombre fini de clauses de longueur finie, les conditions de vérité de tous les énoncés infinis du langage. Ce qui implique que les conditions de vérité des énoncés complexes sont déterminées de manière récursive, sur la base de la structure de l’énoncé et des conditions de vérité de leurs constituants qui, comme nous l’avons vu, sont dans certains cas des formules ouvertes.

La définition de vérité pour L¹ peut être pensée comme une méthode pour expliciter les conditions de vérité de tous les énoncés de L¹, y compris les énoncés atomiques et ceux quantifiés. L’explicitation est pleinement compositionnelle, parce que la valeur de vérité d’un énoncé complexe dépend de celles de ses constituants simples, et la valeur de vérité d’un énoncé simple dépendra des dénotations de ses constituants (non énonciatifs). Par exemple dans le cas d’un énoncé atomique comme “P²ab”, il découle de la définition de Tarski que

(11) l’énoncé “P²ab” est vrai (en L¹) si et seulement si <I(a), I(b)> Œ I(Pⁿ),

ou I(a), I(b), I(Pⁿ) sont les dénotations des expressions “a”, “b”, “Pⁿ”. L’analyse des conditions de vérité – et donc du point de vue du paradigme dominant, l’analyse de la signification – est donc étendue bien au-delà de ce qui avait été fait dans le Tractatus.

Il faut éviter de confondre la conception tarskienne de la vérité – substantiellement, l’idée que chaque définition de vérité pour un langage doit impliquer les biconditionnels de la forme (T) – et la définition particulière de “vrai (en L¹)” que Tarski propose pour exemplifier sa conception. L’expression “théorie de la vérité de Tarski” est employée de manière ambiguë, pour désigner tantôt l’une tantôt l’autre chose. Les rapports entre les deux sont complexes : la définition proposée par Tarski n’est certainement pas la seule qui soit conforme à sa conception de la vérité, et d’autre part – cela paraît évident, mais il est bon de le répéter – le critère d’adéquation matérielle n’est pas une définition de la vérité, mais précisément, un critère pour des définitions de la vérité. Il faut noter, incidemment, qu’un biconditionnel tel que (11) n’est pas de la forme (T) : il s’agira de faire voir que l’on peut en déduire le biconditionnel approprié, mais (11) en soi ne l’est pas, parce que son côté droit n’est pas la traduction métalinguistique de “P²ab”.

En tous cas, c’est la définition de “vrai (en L¹)” qui s’est imposée comme modèle d’analyse sémantique. Non pas pourtant dans le sens, que nous avons tenté de préciser, selon lequel elle constitue une méthode pour expliciter systématiquement les conditions de vérité des énoncés d’un langage ; mais plutôt en vertu de l’appareil référentialiste qu’elle met en évidence. Pendant un certain temps, l’analyse sémantique d’un langage fut plus ou moins identifiée avec son interprétation sémantique, dans le sens de la connexion des expressions simples du langage avec leurs dénotations dans un domaine ; et la théorie sémantique fut identifiée avec la théorie de la dénotation, dite plus généralement théorie de la référence. C’est la conception qui fut acceptée par la définition de Morris (1938 : 57), selon laquelle la sémantique « traite du rapport des signes avec leurs designata et ainsi avec les objets qu’ils dénotent éventuellement ». Tarski lui-même contribua à l’identification de la sémantique avec la théorie de la référence, en écrivant par exemple que « la sémantique [...] s’occupe de certaines relations entre les expressions d’un langage et les objets (ou “états de choses”) “indiqués” par de telles expressions » (Tarski, 1944 : 345). Non seulement Frege, mais également le Tractatus, avec sa notion de sens de la proposition, sont ici oubliés, et prévaut au contraire l’idée selon laquelle fait de spécifier la signification c’est spécifier la dénotation.

14. La théorie sémantique de Carnap.

En 1943, W. V. O. Quine (§ 27-29) tira la communauté philosophique du sommeil référentialiste dans lequel elle était tombée, en soulignant l’écart radical entre la notion de référence qui était à la base de la sémantique tarskienne et la notion intuitive de signification. Si la signification était la référence, fit remarquer Quine, en reprenant une argumentation de Frege (1892b), tous les énoncés vrais de la forme a = b – y compris ceux simplement factuels, tels que “l’Étoile du Matin = l’Étoile du Soir” – affirmeraient une relation de synonymie entre “a” et “b”, qui, en tant que telle, devrait être connue de toute personne parlant avec compétence la langue ; alors qu’il est évident que de telles vérités ne peuvent être établies que grâce à une recherche empirique. D’autre part, les noms dépourvus de référence (comme “Pégase”) ne sont pas pour autant dépourvus de signification : au contraire, c’est précisément grâce à leur signification que nous pouvons être sûrs qu’ils n’ont pas de référence. Dans une série de recensions qui datent approximativement de ces mêmes années, et dans deux importants articles ultérieurs (1951a, 1951b), le logicien Alonzo Church reproposa les idées de Frege sur sens et dénotation, avec une importante simplification (que Frege n’aurait sans doute pas acceptée) : les prédicats ne dénotent pas des concepts, mais directement des classes (par exemple “rond” dénote la classe des choses rondes : Church, 1951b : 108). La notion de concept comme entité non saturée, que Frege avait placée à la base de son analyse des énoncés simples, est ainsi éliminée. Sont par contre réhabilités les sens de Frege, conçus comme entités abstraites objectives, que la sémantique ne peut éluder.

La théorie proposée par Carnap dans Signification et nécessité (1947) présuppose ce regain d’intérêt pour l’édifice frégéen originel, et plus généralement la conscience de l’insuffisance analytique de la sémantique référentielle. À l’intérieur d’une sémantique de type tarskien, les énoncés modaux comme (12)

(12) Nécessairement 9 est plus grand que 7

n’admettent pas une analyse compositionnelle : la valeur de vérité de (12) n’est pas fonction des dénotations de ses constituants. En effet, (12) inclut comme constituants l’énoncé vrai (13) :

(13) 9 est plus grand que 7 ;

mais en remplaçant (13) par un autre énoncé vrai, (14) par exemple :

(14) Paris est la capitale de la France

on obtient (15), qui, à la différence de (12), n’est pas vrai :

(15) Nécessairement Paris est la capitale de la France.

Donc (12) n’est pas compositionnel par rapport à la dénotation (si c’était le cas, le remplacement de constituants équidénotants ne modifierait pas la valeur de vérité) ; ce qui revient à dire qu’une théorie purement référentielle n’est pas en mesure de rendre compte de la structure sémantique de (12), et en général des énoncés modaux. Carnap se propose d’étendre à ces énoncés le traitement compositionnel que Frege, Wittgenstein et Tarski avaient donné du fragment véri-fonctionnel et quantificationnel du langage, en introduisant dans l’analyse sémantique une dimension supplémentaire, correspondant plus ou moins à celle du sens frégéen. Par ailleurs, Carnap ne considère pas comme immédiatement utilisable ce concept frégéen qu’il juge obscur : Frege ne spécifie jamais les conditions d’identité pour le sens, c’est-à-dire qu’il ne dit pas quand deux expressions distinctes ont le même sens (Carnap, 1947 : § 28). Le couple frégéen sens/dénotation doit être remplacé par des concepts rigoureusement définis. En reprenant les termes de Leibniz, Carnap nomme ces concepts intension et extension, et les introduit de la manière suivante : considérons un langage de premier ordre L¹, avec des constantes individuelles (a, b, c, ...), des variables individuelles (x, y, z, ...) et des constantes prédicatives (P, Q, ...), en plus des connecteurs et des quantificateurs. Les énoncés atomiques de L¹ sont de la forme “Q²ab”, dans lesquels un prédicat à n places est suivi de n constantes individuelles. Intuitivement, ces énoncés ressemblent à des énoncés naturels simples comme “Socrate est mortel”, “Turin est plus grand que Clichy-sous-bois”, etc. Appelons maintenant description d’état un ensemble d’énoncés de L¹ qui contient, pour chaque énoncé atomique, soit l’énoncé lui-même soit sa négation (mais non pas les deux ensemble). Par exemple, si L¹ était aussi simple qu’il ait à sa disposition seulement trois constantes individuelles a, b, c, et une seule constante prédicative à une place P, l’ensemble {Pa, ~ Pb, Pc} serait une description d’état (il y aurait en tout huit descriptions d’état possibles dans ce langage). Comme le note Carnap, chaque description d’état en L¹ représente la description d’un monde possible du point de vue de L¹. Une (et une seule) d’entre elles sera la description d’état vraie, c’est-à-dire celle qui représente le monde réel (pour autant qu’il soit accessible aux ressources expressives de L¹). Un énoncé atomique vaut dans une description d’état D si et seulement si il appartient à D ; pour les énoncés complexes, la notion de « valoir dans une description d’état » est définie récursivement (par exemple, dans le cas du micro-langage dont nous parlons, l’énoncé “("x)Px” vaut en D si et seulement si “Pa”, “Pb”, “Pc” valent en D).

Ceci dit, Carnap définit les conditions d’identité pour l’extension et l’intension, c’est-à-dire les circonstances dans lesquelles deux expressions linguistiques ont la même extension (ou la même intension). En commençant par les énoncés, disons que deux énoncés p et q ont la même extension s’ils valent ou ne valent pas tous deux dans la description d’état vraie ; donc p et q ont la même extension si et seulement si ils sont vrais tous les deux, ou faux tous les deux. L’extension d’un énoncé peut donc s’identifier avec sa valeur de vérité (V ou F), comme c’était le cas pour la dénotation chez Frege. Disons au contraire que p et q ont la même intension si p vaut dans toutes les descriptions d’état dans lesquelles vaut q, et réciproquement. Intuitivement, p et q ont la même intension s’ils sont « vrais dans les mêmes mondes possibles », c’est-à-dire dans les mêmes circonstances : connaître l’intension d’un énoncé, c’est savoir dans quelles circonstances il est vrai. De cette manière, Carnap formalise l’idée centrale du paradigme dominant, selon laquelle la signification d’un énoncé s’identifie avec ses conditions de vérité.

Carnap définit les conditions d’identité extensionnelle et intensionnelle également pour les autres catégories d’expressions sémantiquement autonomes (termes singuliers et prédicats) ; en général, deux expressions ont la même intension si,et seulement si, ils ont la même extension dans toutes les descriptions d’états. Par exemple, deux prédicats (à une place) ont lamêmeintension si, dans toutes les descriptions, ils désignent la même classe. Dire que “rêche” et “rugueux” (par exemple) ont la même intension, c’est dire que si, en des circonstances déterminées, un objet mérite d’être défini comme “rêche”, alors il mérite également d’être défini comme “rugueux”, et réciproquement. En termes de définition directe, l’extension d’un terme singulier est un individu, celle d’un prédicat est une classe (Carnap partage avec Church la simplification des idées de Frege) ; l’intension d’un énoncé est dite proposition, celle d’un prédicat propriété, celle d’un terme singulier concept individuel.

Nous disposons maintenant d’une notion définie rigoureusement (l’intension) au lieu de la notion vague de sens proposée par Frege. Ceci nous permet d’analyser de manière compositionnelle également les énoncés modaux : pour ces énoncés, la compositionnalité ne vaut pas au niveau des extensions, mais vaut au niveau des intensions. En d’autres termes, même si la valeur de vérité (l’extension) d’un énoncé comme (12) n’est pas fonction des extensions de ses constituants, l’intension de l’énoncé est au contraire fonction des intensions des constituants. En effet, si dans (12)

(12) Nécessairement 9 est plus grand que 7

nous remplaçons le constituant “9 est plus grand que 7” par un autre énoncé ayant la même intension, par exemple (16)

(16) Aucun nombre premier (à l’exception de 3) n’est divisible par 3

nous obtenons (17)

(17) Nécessairement aucun nombre premier (à l’exception de 3) n’est divisible par 3

qui a non seulement la même valeur de vérité que (12) – la même extension – mais également la même intension. (12) et (17), en effet, ont la même intension si et seulement si ils valent dans les mêmes descriptions d’état (par définition d’intension) ; un énoncé de la forme “Il est nécessaire que p” vaut dans une description d’état si et seulement si “p” vaut dans toutes les descriptions d’état (par définition de nécessité, que Carnap identifie – une fois encore, à la suite de Leibniz – avec la vérité dans tous les mondes possibles) ; ainsi, puisque tant “9 est plus grand que 7” que (16) valent dans toutes les descriptions d’état, (12) et (17) valent tous deux à leur tour dans toutes les descriptions d’état, et donc valent dans les mêmes descriptions d’état : ils ont la même intension (pour une exposition plus détaillée du traitement carnapien de la modalité, voir Casalegno, 1997 : 5.4).

15. Attitudes propositionnelles.

L’efficacité de l’appareil critique de Carnap ne s’étend pas à tous les contextes non extensionnels, c’est-à-dire à tous les énoncés dont l’extension n’est pas fonction des extensions des constituants. Il n’est pas en mesure de traiter des contextes d’attitudes propositionnelles comme (18)

(18) P’tit Pierre n’est pas sûr que 68 + 57 = 125

P’tit Pierre, qui a huit ans, a des doutes quant au résultat de cette addition tandis qu’il est absolument sûr, par contre, que 3 + 3 = 6. Et pourtant “68 +57 = 125” et “3+ 3 = 6”, étant des vérités nécessaires, valent dans toutes les descriptions d’état et ont la même intension. Par conséquent, (18) et (19)

(19) P’tit Pierre n’est pas sûr que 3 + 3 = 6

devraient avoir non seulement la même extension, mais également la même intension. Au contraire, ils n’ont même pas la même extension (c’est-à-dire la même valeur de vérité), parce que le premier est vrai tandis que le second est faux. Les contextes d’attitude propositionnelle ne sont pas compositionnels, pas même par rapport à l’intension.
Pour résoudre cette difficulté, Carnap introduit un nouveau concept, à savoir celui de structure intensionnelle (Carnap, 1947 : § 14-15) ; et il essaie de soutenir que des énoncés tels que (18), bien que n’étant pas compositionnels par rapport à l’intension, le sont par rapport à la structure intensionnelle. Il s’avère en effet que “68 + 57 = 125” et “3 +3 = 6”, tout en ayant la même intension, n’ont pas la même structure intensionnelle (et c’est pourquoi (18) et (19) ne sont pas sémantiquement équivalents). La proposition de Carnap, tout en ayant été reprise également par la suite (par exemple par D. Lewis, 1970), s’est avérée très vite inadéquate : des exemples d’énoncés qui ne sont pas compositionnels, pas même par rapport à la structure intensionnelle, ont été avancés (voir par exemple Bonomi, 1983 : 134 q.), et d’autre part, l’identité de structure intensionnelle (que Carnap appelle isomorphisme intensionnel) est probablement une condition trop restrictive pour rassembler nos intuitions sur la relation d’équivalence sémantique, ou synonymie, entre énoncés. En réalité, le paradigme dominant n’est pas parvenu, pas même par la suite, à venir à bout du problème de la compositionnalité des énoncés d’attitude propositionnelle. Comme nous le verrons (§ 33), il semble qu’ils mettent en évidence une difficulté de fond du paradigme, qui ne se résout pas en inventant des représentations toujours plus affinées de la valeur sémantique d’une expression linguistique (pour une discussion de la question voir Mariani, 1992).

16. Le lexique et les postulats de signification

On dit des énoncés vrais dans toutes les descriptions d’état qu’ils sont “L-vrais” (c’est-à-dire logiquement vrais) ; Carnap présente le concept de L-vérité comme un équivalent rigoureux du concept kantien de vérité analytique (1947 : § 2). Toutefois, comme le fit aussitôt remarquer Quine (1951 : cf. § 27), seule une partie des énoncés communément appelés “analytiques” s’avèrent L-vrais dans le système de Signification et nécessité. Des énoncés comme “Aucun célibataire n’est marié”, dont la vérité ne dépend – intuitivement – que de la signification des mots, et non de celle des mots comme “ou”, “non”, “tous”, etc., mais de celle de mots comme “célibataire” et “marié”, ne sont pas L-vrais : on peut envisager une description d’état où valent à la fois “a est célibataire”, soit “a est marié”. En d’autres termes, le système originel de Carnap ne prévoit pas de liens de compatibilité entre des énoncés atomiques : si deux énoncés sont atomiques, ils peuvent valoir dans la même description d’état, quelle que soit la signification intuitive des prédicats qui y apparaissent. Ainsi, le système n’est pas en mesure de distinguer (sauf dans le cas des vérités logiques au sens strict, comme par exemple “Tous les hommes sont des hommes”) entre énoncés vrais en vertu de la signification des mots et énoncés vrais sur la base des faits mondains ; donc, il ne constitue pas une explication complète de nos intuitions sémantiques. Pour palier à cet inconvénient, Carnap élabore la théorie des postulats de signification (Carnap, 1952), qui représente la seule contribution à la sémantique lexicale (c’est-à-dire à l’étude de la signification des mots) produit dans le cadre du paradigme dominant.

Un postulat de signification est la stipulation d’une relation entre extensions de prédicats. En assertant un postulat comme

(20) Pour chaque x, si x est célibataire, alors x n’est pas marié

nous stipulons que les extensions de “célibataire”et “marié” sont disjointes (c’est-à-dire qu’elles n’ont pas d’éléments communs). Si nous choisissons de faire valoir (20) dans toutes les descriptions d’état – c’est-à-dire de faire de (20) un lien sur les intensions de “célibataire” et “marié” – nous aurons comme conséquence qu’aucune description d’état ne pourra contenir à la fois “a est célibataire” et “a est marié” (pour n’importe quel a). Un énoncé comme “Si Jean-Pierre est célibataire, alors il n’est pas marié” vaudra alors dans toutes les descriptions d’état ; et la notion de vérité analytique coïncidera avec celle de L-vérité, si nous avons asserté des postulats de signification qui saisissent toutes les relations sémantiques entre des unités lexicales. Il est clair en effet que les différentes relations de sens, objet traditionnel de la sémantique linguistique (Lyons, 1977 : I, 9), comme l’hyponymie (“rose” est un hyponyme de “fleur”), la synonymie (“doux” est un synonyme de “soyeux”), l’antonymie (“célibataire” et “marié” sont antonymes) peuvent être exprimées par des postulats de signification.

Comme nous le verrons (§ 27), Quine n’aurait pas apprécié cette solution, en considérant que, de toutes façons, la frontière entre vérités analytiques et vérités factuelles ou synthétiques ne peut être marquée clairement. Pour Carnap, toutefois, un choix de postulats de signification ne reflète pas l’état du langage, mais seulement la décision du théoricien de traiter certaines relations comme analytiques. En prenant une décision plutôt qu’une autre, le théoricien est guidé « non pas par [ses] croyances par rapport aux faits mondains, mais par [ses] intentions concernant les significations » (Carnap, 1952 : 225) : un choix de postulats a une valeur programmatique plus que cognitive. L’âpre conventionnalisme de cette position de Carnap n’a pas empêché que les postulats de signification soient constamment interprétés, par la suite, comme des analyses des significations des mots et non comme des stipulations sur leur emploi dans un système déterminé.

17. La sémantique des mondes possibles et le programme de Montague.

Les analyses sémantiques de Carnap ne s’appliquent pas directement au langage naturel ; elles s’appliquent à des langages formels artificiels (comme notre langage L¹), et au langage naturel dans la mesure où il est reconductible à un langage formel. Un élève américain de Tarski et Carnap, Richard Montague (1930-1970) conçut l’ambitieux projet d’une analyse sémantique directe d’une langue naturelle (l’anglais) qui aurait atteint le même degré de rigueur que les théories sémantiques pour les langages formels, au point de pouvoir être considérée, au plan de tous les effets, comme une théorie mathématique. Le cadre conceptuel de Montague se place dans la continuité de celui de Carnap que nous venons de décrire, mais il utilise – en plus d’une théorie syntaxique plus riche et plus complexe – une théorie sémantique très puissante créée par Saül Kripke (né en 1941), S. Kanger et J. Hintikka à partir du milieu des années cinquante, et connue sous le nom de sémantique des mondes possibles.

La théorie fut élaborée à l’origine pour démontrer les propriétés formelles (complétude, consistance, etc.) des systèmes de logique modale, qui analysent les relations logiques entre énoncés formés avec des opérateurs tels que « Il est nécessaire que », « Il est possible que » : l’implication entre “Il est nécessaire que p” et “p” et celle entre “p” et « Il est possible que p », sont des exemples de telles relations bien connues des philosophes du Moyen Âge. Dans une sémantique des mondes possibles, une expression linguistique est interprétée en relation à un monde possible ; par exemple, on ne dira pas que (dans une certaine interprétation) un énoncé du langage est simplement vrai (ou faux), mais qu’il est vrai (ou faux) par rapport à (ou dans) un monde possible. Si le langage interprété est un langage propositionnel, une interprétation « à mondes possibles » (au sens de Kripke, dont la formulation a été et est toujours la plus influente) est un triplet <W, R, I>, où W est un ensemble de mondes possibles, R est une relation définie sur W (dite relation d’accessibilité) et I est une fonction – structurellement semblable à la fonction I d’une interprétation tarskienne : voir § 13 – qui assigne à chaque énoncé du langage une valeur de vérité par rapport à un monde possible w (appartenant à W). La validité est définie comme vérité dans tous les mondes possibles, dans toutes les interprétations (ou, comme dit Kripke, dans tous les modèles). Si le langage interprété est un langage modal standard, et la possibilité et la nécessité sont interprétées comme (respectivement) vérité dans au moins un monde possible et vérité dans tous les mondes possibles, les formules valables dépendent des propriétés formelles de la relation R : si R est réflexive, les formules valables sont exactement les théorèmes de T (la logique modale « de base » développée par von Wright), si R est réflexive et transitive, les formules valables coïncident avec les théorèmes de S4 (de Lewis et Langford), etc. En ce sens, des structures différentes de l’ensemble des mondes possibles – des R différentes – correspondent à des conceptions différentes de la possibilité et de la nécessité.

Si le langage interprété est un langage prédicatif, les choses se compliquent : l’ensemble des formules valables – et donc l’ensemble des inférences valables – varie selon les assomptions qui se font sur le domaine d’individus associé à chacun des mondes possibles, et donc selon que l’on admette que le domaine est le même pour tous les mondes possibles (dans tous les mondes possibles il y a les mêmes individus, seules leurs propriétés sont différentes), ou au contraire qu’un monde possible peut contenir des individus en plus ou en moins par rapport à un monde donné (ce qui est la position de Kripke).

Le système de Carnap (1947), que nous avons décrit il y a peu (§ 14 q.), est déjà une sémantique des mondes possibles, au sens où l’ensemble des descriptions d’état pour un langage équivaut à un triplet <W, R, I> : dire – par exemple – que I (Pa, w_i) = V revient à dire que l’énoncé “Pa” appartient à la description d’état D_i. Les règles d’évaluation des énoncés modaux chez Carnap correspondent, du point de vue de Kripke, à l’assomption que la relation R soit universelle, c’est-à-dire que chaque monde soit accessible à chacun des autres mondes.

Ceci étant établi, venons-en à la théorie de Montague (dite souvent grammaire de Montague ; pour une exposition, voir Chierchia et McConnell-Ginet, 1990 ; Casalegno, 1997 : chap. 6). Il existe deux versions principales de la théorie : l’une exposée dans L’anglais comme langage formel (1968) et l’autre, aujourd’hui plus souvent appliquée, dans Le traitement correct de la quantification dans l’anglais ordinaire (1970) (ces deux essais et la plus grande partie des autres écrits de Montague sont désormais publiés in Montague, 1974).

Comme on l’a dit, Montague considérait qu’une langue naturelle comme l’anglais pouvait être traitée effectivement comme un langage formel, et que son interprétation sémantique ne différait pas, dans ses grandes lignes, de celle d’un langage logique ; il était donc possible d’expliciter complètement les liens sémantiques reconnus par un locuteur compétent, c’est-à-dire formuler une théorie dans laquelle de tels liens seraient démontrables. Dans une grammaire de Montague, on peut distinguer trois composantes : un module grammatical, qui engendre les expressions bien formées de la langue (les énoncés ambigus admettent plusieurs processus d’engendrement distincts, qui déterminent des structures syntaxiques différentes) ; un module de traduction, qui assigne à chaque structure syntaxique sa traduction dans un langage logique d’ordre supérieur au premier (« logique intensionnelle ») ; et un module d’interprétation, dans lequel les formules du langage logique sont interprétées en structures algébriques complexes (fondées sur la théorie des ensembles) de manière à ce que soient déterminées les conditions de vérité des formules correspondantes aux énoncés anglais, c’est-à-dire leur liens implicatifs. Dans les formulations plus avancées de la théorie, toutes les interprétations sont intensionnelles : la valeur sémantique qu’une interprétation assigne à une expression linguistique est une intension, c’est-à-dire une fonction qui assigne une dénotation à un couple constitué par un monde possible et un contexte d’usage. Dans les systèmes de Montague, le passage à travers un langage logique (la traduction en logique intensionnelle) n’est pas essentiel : il est possible de définir une fonction qui interprète directement les structures syntaxiques engendrées par le premier module. Donc l’anglais est véritablement traité comme un langage formel.

Quand on parle d’interprétation de l’anglais, ou d’une autre langue naturelle, on doit entendre des fragments plus ou moins amples de cette langue : un fragment est délimité par un certain ensemble d’unités lexicales et par des constructions grammaticales déterminées. En d’autres termes, la théorie s’applique à des ensembles (infinis) de phrases formées à partir de mots déterminés selon des règles grammaticales déterminées, qui ne sont pas toutes les règles de formation de la langue ; l’objectif dernier de la théorie est d’arriver à couvrir toutes les constructions grammaticales reconnues (ou, si l’on veut, tous les types de phrases anglaises, ou d’une autre langue) et de résoudre tous les problèmes posés par le lexique de manière telle que l’extension du traitement à de nouveaux mots soit banal. On parle d’une grammaire de Montague pour désigner le traitement d’un fragment déterminé d’une langue selon les principes que nous venons de spécifier ; tandis que la grammaire de Montague est la méthode générale de traitement du langage naturel.

La méthode de Montague réalise pleinement l’idée de compositionnalité de la sémantique. L’interprétation d’une expression complexe est en effet toujours une fonction des interprétations de ses constituants, qui dépend seulement de la structure syntaxique de l’expression complexe. Par exemple, admettons que l’analyse syntaxique de l’énoncé “Le chien court vite” soit représentée par l’arbre suivant (R1, R2, R3 sont des règles syntaxiques : par exemple, le syntagme “le chien” est constitué de “le” et “chien” sur la base de la règle R1. Évidemment nombre d’éléments de l’analyse ne sont pas explicités) :

 L’interprétation de chaque constituant dépend uniquement de celles de ses constituants immédiats : ainsi l’interprétation de “le chien court vite” dépend exclusivement des interprétations de “le chien” et “court vite” et de la règle R3, l’interprétation de “le chien” dépend de celles de “le” et “chien” et de la règle R1 etc. On parle en ce cas de compositionnalité règle par règle : l’interprétation avance pas à pas, en interprétant chaque constituant sur la base de la règle syntaxique à travers laquelle il est formé et des interprétations de ses constituants immédiats. La réalisation de cette compositionnalité parfaite implique quelque sacrifice, entre autres en ce qui concerne le caractère plausible des analyses syntaxiques. Mais Montague était souverainement indifférent aux critiques des chomskyens, pour qui une analyse syntaxique doit être motivée par des considérations purement syntaxiques et ne pas être seulement fonctionnelle à l’analyse sémantique : il déclarait « ne pas trouver grand intérêt à la syntaxe, sinon comme prélude à la sémantique », il était sceptique quant au « relief sémantique » des analyses syntaxiques des générativistes, et considérait les travaux de Chomsky critiquables sur le plan « de l’adéquation, de la précision mathématique et de l’élégance » (Montague, 1970 : 223). En réalité, ce qui séparait Montague des chomskyens était surtout une idée profondément différente des tâches de la théorie linguistique. Pour Montague, la sémantique doit certes rendre compte des intuitions des locuteurs dans le sens où, par exemple, les implications démontrées par la théorie doivent coïncider avec celles reconnues effectivement par les locuteurs ; mais il ne doit pas se préoccuper de reproduire des processus mentaux hypothétiques sous-jacents à l’interprétation sémantique d’un énoncé de la part d’un locuteur. L’idée qu’une règle syntaxique ou une règle d’interprétation sémantique doivent être plausiblement imputables à un esprit fini comme celui de l’homme est tout à fait étrangère à Montague, pour qui la sémantique fait partie de la mathématique et non de la psychologie. Également sous cet aspect, d’antimentalisme radical, la grammaire de Montague constitue la pleine réalisation du paradigme dominant.

18. Trois philosophes

La réflexion sur le langage des années Cinquante-Soixante est dominée par trois grandes figures, qui ont encore aujourd’hui une forte influence et ne sont pas reconductibles au paradigme dominant que nous avons illustré jusqu’à présent, ni même identifiables simplement comme critiques de ce paradigme : il s’agit de Wittgenstein, Austin et Quine. En réalité, l’influence de Wittgenstein précède les autres, parce qu’elle commence à s’exercer à travers l’enseignement à Cambridge (à partir du début des années trente) : mais elle s’étend considérablement après la publication posthume des Recherches philosophiques (1953). Austin agit aussi surtout à travers son enseignement à Oxford. Les deux influences semblent, pour un certain temps, converger en déterminant un style caractéristique de la philosophie britannique, que l’on a appelé tour à tour, “philosophie linguistique”, “philosophie analytique”, “philosophie du langage ordinaire” ou encore – plus prudemment – “philosophie d’Oxford et de Cambridge”. A ce courant, dont nous ne parlerons pas ici de manière thématique, contribuent de nombreux autres philosophes parmi lesquels G. Ryle, P. Strawson, J. Wisdom. Il semble tout à fait clair aujourd’hui que les positions d’Austin et du « second » Wittgenstein furent toujours très différentes, malgré l’intérêt commun pour le langage ordinaire, la méfiance partagée pour les formalisations et d’autres motifs encore également consonants. La pensée de Quine représente au contraire, un résultat (hautement original) de l’émigration américaine du néo-positivisme et de sa rencontre-confrontation avec les instances du pragmatisme.

19. Le « second » Wittgenstein

Dans aucune de ses phases, la pensée de Wittgenstein ne peut être caractérisée comme une philosophie du langage au sens étroit de l’expression : Wittgenstein fut toujours intéressé par les problèmes de la philosophie en général (au début, comme on l’a vu, à ceux de la philosophie de la logique), et il ne pensa jamais que son but ultime serait la formulation d’une théorie du langage (cf. Bouveresse, 1991 : 18). Toutefois, il ne fait pas de doute que le Tractatus logico-philosophicus contient une telle théorie (§ 10-11), quand bien même tend-elle à la clarification des problèmes tels que la nature de la logique ou le statut de l’éthique. On ne peut rien trouver de comparable dans les écrits de la fameuse « seconde phase ». Au cours des années 1929-1933, Wittgenstein se libère graduellement de l’idée même d’une « théorie générale du langage » : la construction d’une telle théorie ne lui apparaît plus comme une condition préalable des analyses philosophiques qu’il entend mener ; au contraire, le projet de saisir l’essence du langage (ou des propositions, ou de la règle, etc.) lui semble être le fruit d’un préjudice métaphysique. Ainsi, les Recherches philosophiques (1953) et les autres écrits postérieurs à 1929 contiennent, en plus d’une myriade d’observations précises et profondes sur les différents phénomènes linguistiques, également des idées qu’il est difficile de ne pas considérer comme des éléments d’une théorie du langage (la notion de ressemblance familiale, parexemple), ou comme des indications sur la forme d’une telle théorie (l’idée de jeu de langage, le slogan « la signification c’est l’usage », la proposition de remplacer les questions sur la signification – « Que signifie “X” ? » – par des questions sur l’explication de la signification – « Comment expliquerons-nous la signification de “X” ? »). À tort ou à raison, ces idées ont eu une très forte influence, et pas seulement dans un sens destructeur (comme nous le verrons dans le cas de Dummett), sur la sémantique philosophique qui suivra.

20. La critique du Tractatus

Comme on l’a vu, le Tractatus reconduisait le langage – tout langage – à un ensemble de propositions qui, si elles sont sensées, sont des fonctions de vérité de propositions élémentaires. Celles-ci, à leur tour, sont des liens de noms dont la connexion reproduit la structure de l’état des choses dont la proposition est l’image. Les noms dénotent des objets (éléments simples des états de choses), et c’est grâce au rapport de dénotation entre noms et objets, et à l’identité de structure entre proposition et état de choses, que la proposition (élémentaire) est en mesure de présenter l’état de choses. Le concept frégéen de dénotation (§ 5) – le rapport entre un nom et ce qu’il désigne – et l’idée que les unités linguistiques « vraies », profondes (les véritables « mots »), sont toutes des noms propres, c’est-à-dire des expressions qui désignent des objets particuliers, sont des éléments cardinaux du cadre théorique du Tractatus. Déjà à partir des années trente, Wittgenstein les critiqua tous deux (1934-1935 : 264-268 ; 1933-1934 : 125-126). Dans les Recherches philosophiques, plus tardives, Wittgenstein fait voir de manière diffuse comment on ne peut attribuer le rôle de fonder la sémantique du langage au rapport de dénotation. Il semble que les définitions ostentives (celles dans lesquelles, en indiquant un objet, on dit « Ceci s’appelle “N” ») soient en mesure d’instituer les significations des mots (et, à travers elles, celles de toutes les expressions du langage). Mais en réalité, une définition ostentive est interprétée à partir de la fonction que l’on sait qu’elle doit avoir, et à partir d’une maîtrise déjà acquise du langage : elle « explique l’emploi – la signification – du mot, quand on sait déjà clairement quelle fonction il doit avoir, en général, dans le langage. Ainsi la définition ostentive : “Ceci s’appelle «sépia’” aidera à comprendre le mot si je sais déjà que l’on veut me définir le nom d’une couleur [...] Pour être en mesure de demander le nom d’une chose on doit déjà savoir (ou savoir faire) quelque chose » (1953 : § 30). Du reste, l’idée de dénotation apparaît maintenant à Wittgenstein comme le résultat d’une hyper-simplification philosophique par rapport aux multiples emplois d’un nom (Ibidem : § 37), et même aux nombreux types d’expressions que nous appelons “nom” (Ibidem : § 38). C’est en tout cas une simplification inacceptable que de traiter tous les mots comme des noms, c’est-à-dire de considérer le rapport entre un nom propre et son porteur (entre “Philippe de Macédoine” et la personne de Philippe de Macédoine) comme archétype de la signification. L’« uniformité dans le mode de présentation des mots » (Ibidem : § 11) masque la variété de leurs fonctions, que Wittgenstein compare à la variété des fonctions des outils qui se trouvent dans une boîte à outils (marteau, tournevis, colle, clous, etc.) ou à la multiplicité des emplois des manettes de commande d’une locomotive (Ibidem : § 12) : elles se ressemblent toutes, et toutes sont faites pour être saisies avec les mains, mais l’une d’elles peut être déplacée continûment, une autre n’a que deux positions, une troisième agit en fonction de la force avec laquelle on l’actionne, etc. L’assimilation de tous les mots à des noms, et de toutes les fonctions sémantiques au rapport de dénomination, est une des sources principales d’erreurs philosophiques, selon Wittgenstein : elle induit par exemple à considérer le lexique psychologique (fait de mots comme “penser”, “entendre”, “comprendre”, etc.) comme une collection de noms, et donc à présumer, pour chacun d’eux, un état ou un processus mental qu’il désigne. Une partie significative des Recherches philosophiques est consacrée à combattre ce préjudice, en montrant que ces mots (“penser”, etc.) ne fonctionnent pas, dans le langage, comme des noms d’états ou de processus (1953 : § 138-184, 431-693 ; Kenny, 1973 : chap. 8).

La critique (et on pourrait même dire la satire) du Tractatus, qui occupe les premières sections des Recherches philosophiques, concerne aussi la théorie des propositions et de leurs relations. Le Tractatus liait étroitement la forme des propositions élémentaires (qui sont toutes des liens de noms) et celle des propositions complexes (si elles sont sensées, elles sont des fonctions de vérité de propositions élémentaires). Quant aux relations entre propositions, ce sont des relations logiques – celles exprimées par la logique élémentaire, propositionnelle et prédicative – ou ne sont pas : les propositions élémentaires sont absolument indépendantes l’une de l’autre. C’est le premier aspect de la doctrine du Tractatus qui est concerné par la critique de Wittgenstein : deux propositions élémentaires (comme “A est rouge” et “A est jaune”) peuvent se contredire (1929-30 : § 76), donc il y a « une construction logique [...] qui ne travaille pas avec l’aide des fonctions de vérité » (Ibidem). Au cours de ces années, Wittgenstein continue de voir dans la logique le filigrane du langage naturel, mais son image de la logique se complique, et ne cessera de se compliquer par la suite. À partir de la moitié des années trente, Wittgenstein utilisera toujours plus souvent le terme “grammaire” pour l’ensemble des règles d’usage des expressions d’un langage. Les relations entre propositions codifiées par la logique (au sens strict) sont tout au plus un sous-ensemble de la grammaire, que Wittgenstein considérera toujours moins significatif.

L’idée de proposition élémentaire sera également abandonnée par Wittgenstein dans le cours des années Trente, parce qu’elle fait également tort à la variété du langage : « Combien de type de propositions y a-t-il ? Par exemple : assertion, question et ordre ? – Il en existe d’innombrables [...] Il est intéressant de confronter la multiplicité des instruments du langage et de leurs modes d’utilisation, la multiplicité des types de mots et de propositions, avec ce qu’ont dit les logiciens (y compris l’auteur du Tractatus logico-philosophicus) de la structure du langage » (1953 : § 23). La théorie des propositions élémentaires faisait partie d’une philosophie du langage qui privilégiait de manière exclusive sa fonction descriptive. Dans les Recherches, elle devient une fonction parmi d’autres : donner des ordres, faires des conjectures à propos d’un événement, inventer une histoire, faire un mot d’esprit, traduire, remercier, saluer, etc.

21. Ressemblances familiales et jeux de langage. Grammaire.

Il se peut qu’au-delà des points de doctrine spécifiques (essentiels, par ailleurs, comme nous l’avons vu), le détachement de Wittgenstein de la philosophie du langage du Tractatus ait sa source principale dans l’abandon de l’attitude essentialiste, c’est-à-dire de la prétention de saisir philosophiquement l’essence du langage et de la proposition. « Toute ma tâche consiste à expliquer l’essence de la proposition » avait écrit Wittgenstein à l’époque du Tractatus (1914-1916 : 22. 1. 1915) ; et le livre, avec sa caractérisation de la « forme générale de la proposition » (1922 : 6.), avait été l’accomplissement de cette tâche. À partir de 1932, lorsqu’il dicte ce qu’on a appelé le Big Typescript, dont a été tirée l’œuvre connue sous le titre Grammaire philosophique, Wittgenstein ne pense plus que le fait de déterminer l’essence du langage, de la proposition et de la règle est une condition pour pouvoir analyser le langage, parler de propositions et identifier des règles, et il en vient à faire l’hypothèse qu’il pourrait s’agir d’une tâche impossible : il n’est pas dit que l’essence du langage (ou de la proposition, ou de la règle) soit. Chaque fois que nous avons affaire à un nom commun (un « terme universel ») comme “langage” justement, ou“proposition” etc. nous donnons pour acquis qu’il soit appliqué sur la base d’une essence commune à tous les objets ou phénomènes pour lesquels le nom est utilisé. Or, dit Wittgenstein, « ce que le nom abstrait indique est bien une affinité entre des objets, mais cette affinité ne consiste pas nécessairement en ce qu’ils aient en commun une propriété ou une partie constitutive. Il se peut qu’elle relie les membres comme les maillons d’une chaîne, de sorte qu’un membre est apparenté à l’autre à travers des membres intermédiaires ; et il se peut également que deux membres immédiatement voisins aient en commun certains traits, ou soient semblables l’un à l’autre, tandis que des membres plus lointains n’aient plus rien en commun et appartiennent toutefois à la même famille [...] Ainsi, il n’existe certes pas quelque chose de caractéristique, qui soit commun à tout ce que nous appelons “jeu”. Mais on ne peut pas dire non plus que “jeu” ait, pour autant, plusieurs significations indépendantes [...] On appelle “jeux” des processus apparentés selon des modes différents, parmi lesquels il y a une multiplicité de passages » (1930-1933 : § 35 ; cf. 1953 : § 66-67). Ceci vaut également, en particulier, pour des mots comme “langage”, “proposition”, “règle”. Ces concepts ne sont pas rigidement délimités, et dans la plupart des cas nous n’avons pas besoin de les délimiter pour les utiliser (1930-1933 : § 72-73 ; cf. 1953 : § 65). S’il était nécessaire de définir “règle”, “proposition”, etc. avant de pouvoir utiliser ces mots dans l’analyse philosophique, il y aurait, en quelque sorte, une philosophie avant la philosophie : ce que Wittgenstein appelle une métaphilosophie. « Mais il n’existe pas de métaphilosophie » dit Wittgenstein (1930-1933 : § 72) et il considère cela comme l’une de ses « pensées-phare ».

La doctrine des ressemblances de famille a été considérée comme une nouvelle théorie des concepts, et, comme telle, elle est à l’origine de la théorie des prototypes de E. Rosch (voir Rosch, 1987), qui est une théorie empirique psychologico-cognitive concernant la représentation mentale de la signification des termes universels (comme “jeu”, “meuble”, “fruit”, etc.). Dans l’économie de la pensée de Wittgenstein, elle représente plutôt le chemin par lequel le philosophe parvient à se libérer de l’obsession essentialiste qui caractérise alors à ses yeux le Tractatus. Elle se déploie en même temps que le développement de la conception radicalement pluraliste du langage, fondée sur l’idée du jeu de langage (1930-1933 : § 26 ; 1933-1934 : 56 ; 1953 : § 23). Il n’y a pas seulement de nombreux types de mots ou de nombreux types de propositions : il y a de nombreux langages. « De nouveaux types de langage, de nouveaux jeux de langage, pourrions-nous dire, surgissent et d’autres vieillissent et sont oubliés » (Ibidem : § 23 ; cf. § 18). Mais – comme nous autorise à le dire la doctrine des ressemblances familiales – « ces phénomènes n’ont nullement quelque chose en commun, sur la base de quoi nous utilisons pour tous le même mot [“langage”] – mais [...] ils sont apparentés l’un avec l’autre, selon de modes nombreux et différents » (1953 : § 65). L’expression “jeu de langage” est employée par Wittgenstein de manière non uniforme. Elle se réfère tour à tour à : (a) des situations imaginaires et très simplifiées d’utilisation de langage rudimentaire, qui sont esquissés pour mettre en évidence tel ou tel aspect de notre utilisation du langage (par exemple 1934-1935 : 144-145 ; 1953 : § 7) ; (b) des utilisations « spécialisées » du langage, en relation avec des buts déterminés et dans le cadre d’activités tout aussi déterminées : raconter des histoires (1953 : § 23), employer des expressions comme “douleur”, “avoir mal” (§ 300), prévoir les actions de quelqu’un (§ 632) (c’est peut-être l’emploi le plus commun de l’expression) ; (c) une utilisation globale du langage : par exemple notre utilisation du langage, en tant que partie de notre forme de vie, en opposition à d’autres utilisations possibles, liées à des conditions de vie différentes et des constellations de buts différents (1953 : § 238, § 264).

Dans toutes ces utilisations, bien que très différentes, l’idée de jeu de langage renvoie à l’idée de règle : les jeux de langage sont constitués par des règles pour l’utilisation de certaines expressions dans certaines circonstances. Le but de la philosophie est la description de ces règles : « Nous ne pouvons faire autre chose que de rédiger des tables de règles » (1929-1932 : 164 ; cf. 1929-1930 : § 1), c’est-à-dire expliciter et enregistrer la grammaire des expressions linguistiques. La philosophie est l’« administratrice de la grammaire » (1929-1930 : § 54). Le mot “grammaire” est également utilisé par Wittgenstein de manière ambiguë, pour indiquer l’ensemble des règles d’utilisation d’une expression (c’est à ce titre que l’on parle de la grammaire de telle expression), mais aussi la description de cette utilisation (1930-1933 : § 23) ; en ce sens la grammaire c’est « le maître-livre du langage » (Ibidem : § 44). La notion de signification est définie à travers celle de grammaire : « La place d’un mot dans la grammaire est sa signification » (1930-1933 : § 23). Au cours de ces années, Wittgenstein parle souvent de la signification d’un mot également comme de son « rôle dans le calcul » (par ex. 1929-1930 : § 152 ; 1930-1933 : § 27), parce qu’il pense le jeu de langage en analogie avec un système formel. Par la suite, il abandonnera ce mode d’expression, qui s’adapte mal à décrire des situations d’utilisation du langage où tout n’est pas réglé, et où les règles peuvent changer. Ce sont en tout cas des manières plus ou moins équivalentes de faire allusion au fait que la signification d’un mot n’est autre que la manière dont il est utilisé, et est donnée par les règles de son utilisation. Il ne faut pas attribuer une portée excessive aux formulations célèbres des Recherches – « Pour une grande classe de cas – même si ce n’est pas pour tous les cas – dans lesquels nous nous en servons, le mot “signification” se peut définir ainsi : la signification d’un mot, c’est son utilisation dans le langage » (1953 : § 43 ; cf. 1930-1933 : § 29 ; 1933-1934 : 127). Ce que Wittgenstein veut dire, c’est surtout que lorsqu’on demande ce que signifie un mot, on veut savoir le plus souvent comment il est utilisé ; et une explication de la signification consiste généralement à proposer des exemples d’utilisation. Mais alors surgit immédiatement le problème de savoir comment est-il possible de connaître la signification d’un mot, étant donné qu’il semble impossible de « saisir d’un coup [son] utilisation complète » (1953 : § 191). De ce problème naîtra la discussion sur l’idée de » suivre une règle » dont nous ne nous occuperons pas ici dans la mesure où elle dépasse très largement le domaine de la philosophie du langage (Kripke, 1981 ; Andronico, Marconi et Penco, 1988 : 199-201). L’issue de la discussion, pour ce qui concerne le langage, semble être que connaître un langage, c’est maîtriser une technique (comme une habileté artisanale ou sportive), et doit être décrit plus comme un savoir-faire que comme un savoir.

Il est clair que les concepts d’utilisation et de grammaire ne sont que les faibles prémices d’une « théorie du langage » : l’indication de décrire l’utilisation, ou d’éclaircir la grammaire d’une expression linguistique ne nous dit pas grand-chose des propriétés ou des relations de l’expression qu’il nous faut prendre en considération. Mais Wittgenstein n’éprouvait pas un grand intérêt pour la théorie du langage en ce sens : de son point de vue, l’indication a surtout une valeur négative et thérapeutique. Veiller à l’utilisation, c’est, avant tout, ne pas présumer de savoir déjà – par exemple par la tradition philosophique – quel type de signification a un mot (par exemple qu’il « exprime un concept » ou une « détermination de l’être », ou désigne « une opération de l’esprit », ou un « processus intérieur », etc.). En second lieu, veiller à l’utilisation, c’est ne pas généraliser à tout le langage un seul modèle sémantique, par exemple celui de la dénotation, en cherchant dans chaque cas quelque chose qui aille à l’expression en question comme, disons, les chiens vont au mot “chien”.

22. La critique du mentalisme. Il n’y a pas de langage privé.

Dans les Recherches philosophiques, et dans d’autres écrits de la seconde période, Wittgenstein combat sans relâche deux thèses, ou attitudes philosophiques, dénommées toutes deux : mentalisme. La première est une thèse psychologique : celle à laquelle nous avons déjà fait allusion, selon laquelle les termes de la psychologie « naïve » (“désirer”, “s’attendre à”, “avoir l’intention de”, etc.) sont des noms d’états ou processus mentaux. La seconde est une thèse sémantique : à savoir que les significations des mots sont, en général, des entités mentales. Il s’agit de deux thèses distinctes, non seulement au sens où l’on peut être d’accord avec la première sans pour autant l’être avec la seconde (qui est plus générale), mais aussi dans le sens où soutenir que l’intention est un état mental (le mot “intention” est le nom d’un type d’état mental) et soutenir au contraire que la signification du mot “intention” – comme de tous les autres mots – est une entité mentale (disons l’idée d’intention), quel que soit son rapport avec la chose même (à savoir l’intention), sont deux choses bien différentes. Contre la thèse psychologique, les arguments de Wittgenstein sont nécessairement particuliers, parce qu’il s’agit de faire voir, dans chaque cas, que les termes psychologiques ne fonctionnent pas dans le langage comme des noms d’états ou processus mentaux. Wittgenstein soutient, par exemple, que la compréhension du langage n’est pas un processus psychique (1953 : § 154) : les expériences vécues, les phénomènes psychiques conscients qui accompagnent de manière caractéristique la compréhension (à supposer qu’il y en ait) ne sont pas la compréhension. Wittgenstein ne nie pas que l’on puisse faire référence à des « mécanismes » mentaux – ou cérébraux – de la compréhension (Ibidem : § 154, 158), même s’il est sceptique quant à l’efficacité explicative de telles références ; mais il soutient que l’emploi que nous faisons de mots comme “comprendre” n’est pas fondé sur la présence ou l’absence de tels mécanismes hypothétiques (nous ne disons pas que quelqu’un a compris en fonction du fait que nous avons relevé le fonctionnement d’un tel mécanisme).

C’est contre la thèse sémantique que Wittgenstein aura recours à l’une de ses machines argumentatives qui le rendront célèbre : il s’agit du fameux « argument contre le langage privé » (1953 : § 243 q. ; voir Bouveresse, 1976 : chap. 4). Wittgenstein essaie d’imaginer un langage dont les expressions assument une signification, dans la mesure où elles sont associées à des expériences vécues par le sujet (admettons que ce soit moi) qui institue le langage : par exemple, l’expression “S” est introduite comme nom d’une de mes sensations déterminées. Un langage de ce genre serait privé non pas au sens où l’est un code secret (qui peut être rendu public à notre gré), mais pour des raisons de principe : les significations de ses expressions ne seraient accessibles à personne d’autre qu’à moi. Wittgenstein montre que quiconque se proposerait de communiquer (avec lui-même) dans un tel langage ne disposerait d’aucun critère pour déterminer si son emploi de ses expressions est correct (Ibidem : § 258) : il n’aurait aucun moyen de savoir s’il les utilise correctement, ou s’il ne fait que croire les utiliser correctement : « Ce qui veut dire seulement que dans ce cas on ne peut parler de “correction” (Ibidem). Mais s’il n’est pas possible d’appliquer le concept d’“utilisation correcte”, on ne peut même pas dire que les expressions de mon langage privé présumé aient véritablement été dotées d’une signification. Le « langage privé » n’est pas un langage. Il semble découler de cet argument que la signification (le fait de signifier) d’une expression linguistique ne puisse être identifiée à sa connexion avec une entité mentale : une telle connexion, en effet, ne peut constituer un critère de correction d’utilisation, ni servir de base à un tel critère. Mais il n’y a pas de signification, s’il n’est pas possible de faire de différences entre des utilisations correctes et incorrectes d’une expression linguistique. Il semble s’ensuivre, en outre, que la compréhension du langage ne puisse être une opération mentale, ou en tout cas qu’elle ne peut consister en la reconnaissance de la connexion entre une expression du langage et une entité mentale déterminée (par exemple dans la « récupération » d’une entité mentale à laquelle l’expression est reliée) : dans la mesure où la connexion n’est pas soumise à un contrôle, nous ne pourrons jamais savoir si nous avons véritablement compris ; ou, en paraphrasant Wittgenstein, nous ne pourrons pas faire de distinction entre comprendre et croire comprendre, et nous ne pourrons dès lors plus parler de compréhension. L’argument contre le langage privé a de nombreuses conséquences, dans différents domaines de la philosophie. Pour la philosophie du langage, il constitue une difficulté pour les théories du langage mentalistes (au second sens), comme pour celles avancées par les cognitivistes (voir infra § 33) ; et, en effet, il a été critiqué et rejeté par Fodor (1975 : 70-71) pour ne citer qu’un exemple. L’image du langage qui est certainement impliquée, et peut-être même présupposée, par l’argument contre le langage privé est celle d’une collection d’outils intrinsèquement publics, pour lesquels la possibilité d’être utilisé de manière incorrecte est essentielle, non pas par rapport à des valeurs fonctionnelles préétablies (l’efficacité communicative, par exemple), mais par rapport à une norme déposée dans l’utilisation d’une communauté. (Pour une exposition plus développée, mais encore introductive des idées sur le langage du « second » Wittgenstein, cf. Penco, 1992).

23. La philosophie du langage de Dummett.

Le philosophe anglais M. A. E. Dummett (né en 1925) a tenté une médiation complexe entre les instances du paradigme dominant et certains aspects de la pensée du second Wittgenstein. Du paradigme dominant, il retient surtout le projet d’une théorie de la signification (dont Wittgenstein contestait l’utilité et l’idée même, cf. § 19) ; et il tire essentiellement de Wittgenstein les qualités qu’une telle théorie doit satisfaire. En premier lieu, pour Dummett, une théorie de la signification doit répondre à la question : « En quoi consiste comprendre la signification d’un énoncé ? » et doit être – en ce sens – une théorie de la compréhension. La signification, en effet, n’est rien d’autre que ce qu’une personne qui parle connaît d’une expression, du fait qu’elle la comprend. En second lieu, la théorie doit rendre compte du caractère public de la signification : elle doit représenter la connaissance de la signification comme une compétence contrôlable, qui doit donc se manifester dans des comportements publics, c’est-à-dire dans l’utilisation. L’idée que la connaissance de la signification d’une expression doit pouvoir se manifester pleinement dans l’utilisation découle, pour Dummett, à la fois de l’élaboration du slogan wittgensteinien « la signification c’est l’utilisation », et de la réflexion sur une thèse de Frege connue comme principe de contextualité, selon laquelle « un mot est donné pour quelque chose uniquement dans le contexte d’un énoncé » (Dummett, 1973b : 192-196). Selon Dummett, la thèse est justifiée par le fait que l’énoncé est l’unité linguistique minimum permettant d’accomplir un acte de langage (voir § 25), c’est-à-dire un acte concret de communication ; du reste, l’acquisition de la signification d’un mot advient en observant des exemples de son utilisation dans des énoncés, et la connaissance du sens d’un mot ne peut être démontrée qu’en l’utilisant (c’est-à-dire en montrant que l’on est en mesure de formuler des énoncés dans lesquels il est utilisé correctement). Donc la thèse de la contextualité est étroitement liée à l’idée du caractère public de la signification, qui, à son tour, forme un tout avec la thèse de la manifestabilité dans l’utilisation (sur cet entrelacs théorique, voir Santambrogio, 1986 : 10-18).

Dummett adhère au paradigme dominant également de par son insistance sur le caractère systématique de la théorie de la signification. La compréhension du langage a une nature compositionnelle (§ 6) : notre capacité à comprendre une infinité d’énoncés que nous n’avons jamais rencontrés auparavant ne peut que provenir de la maîtrise de principes concernant la manière dont chaque mot contribue à déterminer la signification des énoncés dans lesquels il apparaît. La théorie de la signification doit rendre compte de ces principes. Et Dummett se range du côté du paradigme dominant, et contre Wittgenstein – ou contre une interprétation diffuse de Wittgenstein – également du fait qu’il considère comme indispensable la distinction frégéenne entre sens et force (§ 6). Si l’on admet, en effet, que la signification d’un mot, c’est sa contribution à la signification des énoncés dans lesquels il apparaît, mais si l’on refuse la distinction entre sens et force, il s’ensuit que « les mots d’un énoncé impératif [doivent] avoir une signification de type complètement différent de celle que les mêmes mots ont quand ils apparaissent dans un énoncé optatif ; ce qui est absurde » (Dummett, 1978 : 449). Si – comme Wittgenstein – on se refuse à reconnaître que la signification conventionnelle d’une assertion, d’un ordre, d’une question etc. dépend (également) de principes généraux qui concernent les assertions, les ordres, les questions en tant que tels, on perd un aspect important de la systématicité et l’on finit par mettre sur le même plan des composants très différents du contenu communicatif d’un énoncé.

Une théorie de la signification est donc constituée d’une théorie du sens (qui en constitue le noyau) et d’une théorie de la force (qui s’occupe des conditions auxquelles un énoncé constitue une assertion, une question, un ordre, etc.). Comme nous le savons, Frege et le paradigme dominant ont considéré que la notion centrale de la théorie du sens, c’est celle de la vérité : le sens d’un énoncé s’identifie avec ses conditions de vérité. La contribution principale de Dummett consiste à se demander si, et éventuellement en quel sens, cette conception est compatible avec les qualités qu’une théorie de la signification doit satisfaire : avant tout l’idée qu’elle doive rendre compte de la compréhension du langage, et le caractère public de la signification (qui implique la manifestabilité de sa connaissance).

D’un point de vue frégéen, la compréhension d’un énoncé s’identifie avec la connaissance de ses conditions de vérité (une connaissance qui, pour diverses raisons, doit être considérée comme largement implicite). Cette connaissance peut toutefois consister en un ensemble d’états ou de dispositions mentales privées : pour le réquisit de la manifestabilité, la connaissance du sens doit pouvoir s’exprimer en actes publics de reconnaissance, que les conditions de vérité d’un énoncé soient satisfaites ou ne le soient pas. En d’autres termes, celui qui est en mesure de reconnaître qu’un énoncé est vrai (quand il l’est) ou qu’il n’est pas vrai (quand il ne l’est pas), démontre qu’il comprend un tel énoncé. Or, il y a des énoncés dont nous ignorons s’ils sont vrais ou faux, et pour lesquels nous ne disposons d’aucune méthode pour l’établir : des énoncés contenant des quantifications sur des domaines infinis (« Il existe au moins un nombre parfait impair »), des énoncés au passé (« Le 6 juillet 1467, il y avait 92 maraîchers sur la place du marché à Clichy »), des conditionnels contrefactuels (« Si Chirac avait gagné les élections législatives, Philippe Séguin n’aurait pas été élu président du RPR »). Pour Frege (§ 6) et les défenseurs de la conception « classique », ou réaliste, de la vérité, les conditions de vérité de ces énoncés sont en tout cas parfaitement déterminées ; et, quoi qu’il en soit, une éventuelle connaissance de telles conditions de vérité ne pourrait d’aucune manière s’exprimer en actes de reconnaissance de la vérité ou fausseté de ces énoncés. Si le concept de vérité pertinent pour la théorie du sens est celui classique (réaliste, frégéen), une théorie du sens qui voudrait être une théorie de la compréhension – pour laquelle, les conditions de vérité doivent être connaissables, ne serait-ce qu’implicitement – viole le réquisit de manifestabilité.

Par conséquent, soit le concept de vérité n’est pas le concept central de la théorie du sens, soit il doit être conçu différemment de la manière dont le concevait Frege (et avec lui le paradigme dominant). Dummett choisit la seconde voie, et propose d’identifier la vérité avec l’assertabilité (sur l’exemple de la conception de la vérité mathématique soutenue par les intuitionnistes) : la connaissance du sens d’un énoncé s’identifiera alors avec la connaissance de ses conditions d’assertabilité. Comprendre un énoncé ce n’est pas connaître la condition qui le rendrait vrai dans le sens du réalisme ; c’est, au contraire, savoir dans quels cas nous serions disposés à asserter l’énoncé, c’est-à-dire qu’est-ce qui vaudrait, pour nous, comme justification de l’énoncé. Toutefois, un énoncé peut être justifié pour des raisons très diverses : la conception de Dummett (qu’il appelle antiréalisme) entraîne le risque du holisme sémantique, c’est-à-dire que l’on puisse faire dépendre le sens d’un énoncé du langage tout entier auquel il appartient. Dummett refuse le holisme, qu’il juge par ailleurs incompatible avec la manière dont le langage est acquis ; sa position semble donc soutenable à la seule condition que la justification d’un énoncé soit toujours reconductible à une justification qui reflète la structure de l’énoncé (dans le sens ou, par exemple, “p et q” est justifié sur la base de p et de q), c’est-à-dire à un « procédé argumentatif dont la compréhension est immédiatement contenue dans notre compréhension de la signification de l’énoncé en question » (Moriconi, 1992 : 282). C’est un réquisit très fort, qui semble difficile à satisfaire (sur cette difficulté voir Moriconi, 1992, et Picardi, 1992 : 305 q.).

24. L’analyse du langage ordinaire.

Bien que J. L. Austin (1911-1960) soit aujourd’hui surtout célèbre pour sa théorie des actes de langages (et pour celle des performatifs dont elle découle), le centre de son travail philosophique est plutôt représenté par ce que l’on a appelé « l’analyse du langage ordinaire » (voir Leonardi, 1992 : 136-139 et plus amplement Graham, 1977 : 8-52) qu’il aurait préféré quant à lui nommer « phénoménologie linguistique » (Austin, 1956-1957 : 144). Austin pensait que toute enquête philosophique devait commencer par un inventaire le plus complet possible du matériau linguistique pertinent pour le problème choisi : il s’agissait de rassembler tous les mots, et les constructions linguistiques, que l’utilisation ordinaire associe au problème, puis de vérifier avec la plus grande précision, dans quelles circonstances et avec quelles intentions nous utiliserions chacune des expressions inventoriées (« ce que nous dirions quand », Austin, 1956-1957 : 143), sans perdre de vue les subtiles distinctions internes au lexique, comme celle entre faire quelque chose « par inadvertance », « involontairement », « impulsivement », « inconsciemment », « accidentellement », « par erreur », etc. Dessiner la carte d’un territoire conceptuel en reparcourant les distinctions tracées par le langage ordinaire est, pour Austin, quasiment tout le travail du philosophe : en effet, « notre réserve commune de mots contient toutes les distinctions que les humains ont jugé utile de faire, et toutes les relations qu’ils ont jugé utile de marquer au fil des générations – puisqu’elles ont résisté au long test de la survie du plus apte, elles sont probablement plus nombreuses et plus valables et plus subtiles [...] que celles que nous pourrions, vous et moi, trouver, installés dans un fauteuil par une belle après-midi – alternative méthodologique la plus largement appréciée » (Austin, 1956-1957 : 144). Quasiment tout, parce que le langage ordinaire (a) est organisé du point de vue d’intérêts pratiques plus que théorétiques, (b) parce qu’il est fondamentalement pré-scientifique, (c)parce qu’il intègre quelquefois « toutes sortes de superstitions, d’erreurs et de fantasmes » (Ibidem : 148). Par conséquent, il n’est pas le dernier mot en philosophie, mais – rappelle Austin – il est le premier.

En réalité, vérifier les circonstances d’utilisation d’une expression linguistique est une opération qui donne lieu à des controverses. Devons-nous dire (par exemple) que le mot “sorcière” désignait des femmes qui avaient fait un pacte avec le diable, ou des femmes dont on pensait qu’elles avaient fait un pacte avec le diable, ou encore qui avaient tel ou tel comportement, ou encore autre chose ? Même si le langage ordinaire est comme un philosophe qui a eu beaucoup de temps à sa disposition, il n’est pas dit qu’il soit facile d’en établir la doctrine. Austin était conscient du fait que l’analyse du langage ordinaire pouvait avoir des issues divergentes, mais il invitait à ne pas dramatiser les choses : « Si nos utilisations ne s’accordent pas [...] nous pouvons trouver pourquoi nous ne nous accordons pas : c’est parce que vous choisissez de classifier d’une certaine manière, et moi d’une autre ». Différentes déterminations des circonstances d’utilisation correspondent à des schémas conceptuels différents (1956-1957 : 146) : vérifier et localiser les divergences est, quoi qu’il en soit, « très éclairant ». Comme le « second » Wittgenstein, Austin ne pensait pas que l’utilisation ordinaire était absolument souveraine (elle était le premier mot et non pas le dernier), ni que sa détermination était univoque. Il pensait, toutefois, que la réflexion sur l’utilisation des mots – le déplacement du niveau de l’enquête philosophique des « choses elles-mêmes », ou des concepts et des essences, aux mots – avait de nombreux avantages, à commencer pas l’identification et la précision des points de divergence entre des visions du monde. L’analyse du langage ordinaire, de ce point de vue, partage nombre de motivations du « passage au mode formel » de Carnap et de la « montée sémantique » de Quine.

25. Performatifs et actes de langage.

Comme nous l’avons déjà fait remarqué (§ 2), dans l’essai Les autres esprits (1946), Austin réfléchit sur des questions que l’on range aujourd’hui sous le titre général d’« autorité de la première personne » : puis-je me tromper quand j’affirme des énoncés (à la première personne) comme “J’ai mal”, ou “Je vois quelque chose de rouge” ? Dans le cours de ses réflexions, Austin fut amené à souligner le caractère non descriptif d’énoncés tels que “Je le sais” : quand je dis “Je le sais” je ne suis pas en train de décrire mon état intérieur comme un état de connaissance exceptionnelle (supérieure même à l’extrême sécurité) ; je donne aux autres ma parole, c’est-à-dire que je leur donne mon autorité pour affirmer ce que je dis savoir (Austin, 1946 : 71 q.). De la même manière, quand je dis “Je le promets”, je ne décris pas mon action, mais je suis en train de l’accomplir. Ces « phrases rituelles » – qui présupposent l’existence d’un rite, c’est-à-dire d’une pratique socialement reconnue et au moins en partie codifiée – ne peuvent à la rigueur être fausses, même s’il peut se trouver que les circonstances ne sont pas telles qu’elles puissent consentir à l’accomplissement du rite : je ne peux pas offrir X (en disant “Je t’offre X”) si X n’est pas à moi, de même que je ne peux pas ordonner quelque chose à quelqu’un, si je ne suis pas dans une position d’autorité par rapport à lui.

Dans les leçons d’Oxford des années 1952-1954, puis dans les William James Lectures de 1955 (sur les notes desquelles est fondé le livre Quand dire c’est faire, 1962), Austin donna une formulation accomplie et indépendante de ces idées, en introduisant quelques modifications terminologiques. Il appela performatifs (c’est-à-dire « exécutifs ») ces énoncés qui ne décrivent ni ne constatent rien (et donc ne sont ni vrais ni faux), mais dont l’émission implique ou s’identifie à l’exécution d’une action. En disant : « Je parie cent francs qu’il pleuvra demain », on n’affirme rien, mais l’on fait quelque chose (dans ce cas, un pari) : on accomplit bel et bien une action, qui modifie la réalité (en particulier le rapport entre les personnes). Pour que cela advienne, toutefois, il faut que soient rassemblées certaines conditions (dites conditions de félicité du performatif) : il faut qu’il y ait une procédure socialement acceptée (comme l’« institution » du pari) dont l’émission de l’énoncé fait partie, qui se déroule correctement et complètement, et que l’énoncé soit émis dans les circonstances et par les personnes appropriées.

Si ces conditions ne sont pas satisfaites, l’acte est nul. En outre, si celui qui émet l’énoncé n’a pas la bonne attitude (par exemple, promet mais ne compte pas maintenir sa promesse) ou ne se comporte pas de manière cohérente avec ses dires par la suite, le performatif est sans doute réussi – une promesse non sincère ou non maintenue reste une promesse – mais, dit Austin, il est abusé. Les énoncés descriptifs normaux, qui sont vrais ou faux (comme « les concombres sont des cucurbitacées ») sont au contraire des constatifs.

Austin essaya de caractériser les performatifs, sur la base de la forme syntaxique, du matériau lexical, etc. sans obtenir de résultat absolument satisfaisant : les performatifs sont souvent à la première personne du singulier du présent de l’indicatif actif (« Je promets que je viendrai jeudi », « Je déclare ouverte la huitième foire de Villeurbanne »), mais pas toujours (« Interdit de cracher par terre », « Les voyageurs avec une grande valise sont priés d’emprunter les passerelles métallisées ») ; certains verbes (verbes performatifs) ont fréquemment une utilisation performative, mais également des utilisations non performatives (« Souvent je promets sans être en mesure de tenir mes promesses »). Ces difficultés l’incitèrent à abandonner la théorie des performatifs pour un point de vue plus général, selon lequel chaque énonciation a un aspect performatif, ou, comme il le dit, illocutoire. Telle est la théorie des actes de langage (sur la transition de la théorie des performatifs à la théorie des actes de langage, voir Récanati, 1981 : 81-87). Un acte de langage est une action d’utilisation du langage de la part d’un locuteur (scripteur, etc.) : Austin considère l’acte de langage comme « le seul phénomène réel » du langage (1962), et donc le seul objet propre d’une théorie du langage. En accomplissant un acte de langage (par exemple en disant : « Je te jure que je viendrai demain »), on accomplit simultanément trois actes distincts : un acte locutoire (locutionary) (l’acte de dire ces mots déterminés), un acte illocutoire (illocutionary) (l’acte que l’on accomplit en disant cette phrase : dans notre cas, la prise d’engagement), et un acte perlocutoire (perlocutionary), c’est-à-dire une action sur l’interlocuteur, qui a sur lui des effets déterminés (par exemple celui de l’épouvanter, de le réjouir, ou de le mettre dans l’embarras). À son tour, l’acte locutoire ou locution a trois aspects : phonétique (la production d’une séquence de sons), phatique (la production de mots et de phrases en tant qu’elles appartiennent à une langue déterminée, elle-même déterminée par un lexique et une grammaire) et rhétique (l’emploi de ces mots ou phrases avec un sens déterminé et une référence déterminée).

Austin prétendait (a) traiter les assertions, objet quasi exclusif de l’analyse du paradigme dominant, exactement comme une classe d’actes de langage à côté des autres (ordres, promesses, excuses, etc.) ; (b) reformuler la doctrine du sens et de la référence – c’est-à-dire la théorie sémantique dominante – « dans les termes de la distinction entre actes locutoires et illocutoires ». De cette manière il proposait la théorie des actes de langage comme théorie générale du langage, dont la sémantique dominante, opportunément réélaborée, aurait constitué un chapitre. De fait, Austin n’accomplit que partiellement le point (b) de son programme. Il fit là aussi des remarques intéressantes, comme par exemple interpréter les assertions dont la présupposition est fausse (« Toutes ses vaches sont noires et blanches » à propos de quelqu’un qui n’a pas de vache) comme insatisfaites, c’est-à-dire en reportant un phénomène sémantique « classique » à sa théorie des forces illocutoires. Mais en général le niveau sémantique ne fut pas atteint par l’analyse d’Austin, et sa théorie fut toujours plus souvent conçue comme une intégration de la théorie sémantique que comme une généralisation destinée à l’absorber. Surtout à partir des années soixante-dix, cette intégration est considérée comme faisant partie de la pragmatique. Plus précisément, la pragmatique – que Morris avait considéré comme une des trois parties de la sémiotique, et caractérisé comme « science de la relation des signes avec leurs interprètes » (1938 : 6, 30) – est toujours plus souvent interprétée comme comprenant la théorie des actes de langage. La pragmatique, en effet, est l’étude de la dépendance de ce qui est dit du contexte dans lequel il est dit ; et l’étude des conditions de réussite des actes de langage montre qu’une telle réussite dépend d’éléments contextuels (intentions du locuteur, expectatives de l’interlocuteur, position réciproque du locuteur et de l’interlocuteur, etc.) (Stalnaker, 1972 : 383-384).

Austin avait distingué cinq classes d’actes de langage consistant dans le fait de proférer un énoncé, sur la base de la force illocutoire de l’énoncé proféré : verdictifs, comme les jugements ; exercitifs, comme les jugements qui portent sur ce qui devrait être fait ; commissifs (les promesses par exemple) ; comportatifs, comme les excuses ; expositifs, comme les démonstrations. Les assertions sont un type d’expositifs : elles s’avèrent être un sous-groupe de sous-groupe d’acte de langage. Une classification partiellement différente fut proposée ensuite par le philosophe américain J. R. Searle (né en 1932) : celui-ci distingua (Searle, 1975b) des actes représentatifs, comme les assertions, directifs, comme les ordres, commissifs, comme les promesses, expressifs, comme les excuses, déclaratifs, comme les nominations ou les candidatures. Searle, qui fut un élève d’Austin à Oxford, apporta à la théorie des actes de langage un esprit systématique qu’Austin n’avait pas eu. Dans son premier livre (Les Actes de langage, 1969), il soumit à une certaine révision la théorie d’Austin des conditions de félicité des actes illocutoires, en analysant en détail (à titre d’exemple) l’acte de la promesse, dont il identifia neuf conditions de réussite. On doit également à Searle l’introduction de la notion d’acte de langage indirect (Searle, 1975a ; voir aussi Récanati, 1981 : 141-199) : le fait de demander de passer le sel, par exemple, peut être exprimé sous une forme d’une question : « Peux-tu me passer le sel ? » Les illocutions indirectes sont analysées par Searle à travers la théorie de la conversation de Grice (§ 26). Plus nettement qu’Austin, Searle refusa la distinction entre sémantique et pragmatique, en considérant que signifier et dire quelque chose qui est doté d’une signification, sont des aspects de l’illocution, et rentrent de fait dans le champ de la théorie des actes de langage. Mais il ne parvint pas non plus à supplanter la théorie sémantique dominante : ses analyses de la référence et de la signification (Searle, 1969 : 64-66, 83-90) sont des analyses de ce qu’est, respectivement, se référer à X et signifier quelque chose à travers Y, mais n’entrent pas dans la substance du contenu sémantique exprimé, et ne répondent pas aux questions auxquelles une théorie sémantique doit répondre.

26. Grice : signification et intention.

Dans la théorie des actes de langage de Searle, le concept d’intention tient une place centrale : la description d’un acte de langage fait une référence essentielle aux intentions de celui qui parle. En cela, Searle adhère à l’orientation d’un autre de ses professeurs à Oxford, H. P. Grice (1913-1988). Dans une série d’articles des années cinquante et soixante (Grice, 1957, 1968, 1969), celui-ci avait proposé une réduction de la notion de signification à celle d’intention (et de fait une réduction de la sémantique à la psychologie, quand bien même était-ce à travers un concept relativement obscur comme celui d’« intention »). « Le locuteur A signifie quelque chose à travers l’expression X » est analysé comme « A a l’intention que l’émission X produise un certain effet chez l’interlocuteur, sur la base de la reconnaissance de cette intention ». Ayant ainsi défini la signification qu’un locuteur entend véhiculer en une occasion donnée, Grice reconduit à cette utilisation les autres utilisations de “signification non naturelle”, ou “signification_nn” et de “signifier_nn” (une « signification non naturelle » c’est typiquement celle linguistique ; « signification naturelle », c’est au contraire, celle à laquelle on se réfère quand on dit par exemple : « Ces taches rouges signifient la rougeole ») : « X signifie quelque chose (dans une occasion déterminée) », « X signifie (dans une occasion déterminée) que ... », « X signifie (intemporellement) quelque chose », etc. Au schéma analytique fondamental de Grice on a opposé différents contre-exemples, qui n’ont fait que le rendre plus compliqué (voir Leonardi, 1992 : 162-166), au point qu’on a pu même désespérer de sa possibilité de réussite.

La notion des intentions du locuteur fait également partie de manière essentielle de l’autre proposition théorique importante de Grice, à savoir la théorie de la conversation (voir Leonardi, 1992 : 166-170 ; Levinson, 1983 : chap. III), formulée dans les William James Lectures de 1967, puis publiée, tout d’abord partiellement sous le titre Logique et conversation (Grice, 1975) et enfin dans sa totalité dans Grice, 1989. La théorie de la conversation veut rendre compte des multiples aspects de la « signification globale » d’un énoncé qui ne sont pas saisis par une analyse sémantique en termes de conditions de vérité. Selon Grice, pour rendre compte de ces excédents communicatifs, il n’est ni nécessaire ni utile de multiplier les sens des expressions linguistiques en fonction du contexte dans lequel elles sont utilisées ; il s’agit, au contraire, de déduire de tels excédents d’une caractérisation systématique de l’interaction entre la signification conventionnelle d’une expression linguistique et le contexte de la conversation. Pour Grice, la conversation est une entreprise rationnelle coopérative, soutenue par un principe (principe de coopération) qui impose d’apporter sa propre contribution à une conversation qui soit fonctionnelle en vue de son bon déroulement. Le principe se définit par quatre groupes de maximes : maximes de la quantité (par exemple : ne sois pas réticent), de la qualité (par exemple : ne dis pas ce que tu crois être faux), de la relation (sois pertinent), du mode (par exemple : évite l’ambiguïté). Bien évidemment ces maximes peuvent être violées ; mais si elles le sont d’une manière voyante ou délibérée, sans que par ailleurs, le locuteur donne l’impression de vouloir « sortir de la coopération » celui qui écoute essaiera de réconcilier le comportement du locuteur avec l’hypothèse qu’il est en train de coopérer, et imaginera qu’il aura voulu communiquer quelque chose d’autre, au-delà de ce que ses mots signifient littéralement et à travers eux. Par exemple, si dans une lettre de recommandation pour un doctorat de recherche on se contente d’affirmer que « le candidat sait utiliser correctement le français et a suivi assidûment les cours », on viole de manière très évidente une maxime (de la quantité : « Ne sois pas réticent »). Il est facile d’imaginer que celui qui écrit a pensé exploiter la maxime pour communiquer le fait qu’il n’avait rien de très élogieux à dire sur le candidat. Cette partie implicite de la communication est nommée par Grice implicature. Il s’agit ici d’une implicature conversationnelle, c’est-à-dire dépendante de l’interaction entre la signification conventionnelle des mots employés et la structure de la conversation ; et d’une implicature particularisée, c’est-à-dire dépendante du contexte spécifique que nous avons imaginé. Il y a aussi des implicatures (conversationnelles) généralisées, qu’une expression fait surgir dans n’importe quel contexte normal dans lequel elle est utilisée. Par exemple, normalement en disant : “Ou p, ou q”, on montre que l’on ne sait pas lequel des deux (de p et q) est vrai : on viole une maxime de la quantité (« Que ta contribution soit aussi informative que l’exigent les circonstances ») sans quoi on serait contraint de violer une maxime de la qualité (« Ne dis rien dont tu n’aies pas la preuve formelle » Grice, 1989 : 46). Selon Grice, un interlocuteur (tout comme l’analyste du langage) doit être en mesure de déduire une implicature conversationnelle de la signification conventionnelle de ce qui a été dit, plus la considération du contexte, plus les règles de la conversation, plus l’hypothèse que celui qui parle a l’intention de se conformer au principe de coopération ou ait eu tout de même l’intention de violer délibérément une maxime. Dans ce sens, Grice dit que les implicatures conversationnelles sont calculables. Toutefois, le calcul d’une implicature n’est pas un processus déductif : il s’agit plutôt d’une « abduction » ou « inférence à la meilleure explication » du comportement de celui qui parle.

À côté des implicatures conversationnelles, Grice place les implicatures conventionnelles, qui font partie de la signification conventionnelle de ce qui est dit : par exemple, l’opposition entre p et q est une implicature conventionnelle des énoncés de la forme “p mais q” (et c’est ce qui distingue le mot mais du mot et). La notion d’implicature conventionnelle repropose la distinction de Frege (§ 5) entre sens et tonalité : tout comme la tonalité, l’implicature conventionnelle est cet aspect de la signification d’une expression qui ne fait pas de différence pour les conditions de vérité des énoncés dans lesquels elle apparaît, et fait pourtant partie de ce que l’expression communique dans n’importe quel contexte (pas seulement dans n’importe quel contexte normal, comme l’implicature conventionnelle généralisée). Du point de vue de la théorie de Grice, l’introduction des implicatures conventionnelles représente la reconnaissance honnête de l’impossibilité de réduire la totalité de la signification linguistique au binôme conditions de vérité/règles de la conversation.

27. Quine : la critique de la notion de signification.

Formé au contact étroit des néo-positivistes (et de Carnap en particulier), le philosophe américain W. V. O. Quine (né en 1908) devint l’un des principaux fossoyeurs de ce mouvement philosophique, dont il critiqua certaines thèses centrales : le conventionnalisme, le réductionnisme, la séparation nette entre enquêtes conceptuelles (du ressort de la philosophie) et enquêtes factuelles (de celui des sciences naturelles). Malgré cela, Quine resta toujours fidèle non seulement aux instances de clarté et de rigueur argumentative caractéristiques du néo-positivisme, mais à l’idée que les sciences de la nature, la mathématique et la logique étaient le « noyau dur » de la connaissance humaine, et constituaient un modèle linguistique et non plus seulement épistémologique. En ce sens, on peut considérer sa critique comme « interne », sinon au positivisme comme doctrine, du moins à nombre de ses motifs d’inspiration. La pensée de Quine a été un des facteurs qui ont déterminé l’évolution du courant principal de la philosophie anglo-saxonne depuis le néo-positivisme jusqu’à l’ample et variée koiné, désignée sous le nom de “philosophie analytique”.

Comme on l’a déjà rappelé (§ 14), au début des années quarante, Quine intervint dans la discussion sur la théorie sémantique en montrant que la notion intuitive de signification n’est pas réductible à celle de référence (le terme de Quine est “désignation”) ; par conséquent, une théorie de la référence comme la « sémantique » tarskienne n’est pas en mesure de saisir complètement nos intuitions sur la signification. On a vu comment ces considérations de Quine, en même temps que celles, presque contemporaines, de Church, ont suscité une reprise d’intérêt pour des notions sémantiques non extensionnelles comme la notion frégéenne de sens ; un intérêt qui culmine dans l’œuvre de Carnap, Signification et nécessité (1947). Quine, de son côté, prit un chemin différent. Au lieu de chercher une explication scientifiquement acceptable de la notion intuitive de signification, il fit voir, dans l’essai Deux dogmes de l’empirisme (1951) et dans d’autres écrits, qu’aucun concept de ce genre ne pouvait être défini ; ou en tout cas qu’aucun des candidats en liste n’était acceptable. Quine raisonne ainsi : la théorie de la signification, plutôt que de s’occuper d’êtres mystérieux nommés « significations », doit rendre compte de la relation de synonymie (identité de signification) entre des expressions linguistiques, et de la propriété, dite analyticité (une assertion est analytique si elle est vraie en vertu de la signification des mots qui la constituent, et non en vertu de l’état des choses dans le monde). En commençant par cette dernière notion, nous observons qu’il y a deux types d’énoncés analytiques : les premiers sont ceux que le système de Carnap est en mesure de traiter (voir § 14), à savoir les vérités logiques, comme :

(21) Aucun homme non marié n’est marié,

qui restent vraies pour n’importe quelle substitution des mots non logiques apparaissant dans l’énoncé (« Aucun philosophe non paralytique n’est paralytique » n’est pas moins vrai que (21)). Mais il existe d’autres énoncés qui sont communément déclarés analytiques : par exemple ceux du type :

(22) Aucun célibataire n’est marié.

Ces énoncés se réduisent à des vérités logiques en remplaçant certains mots par leurs synonymes (dans le cas de (22), en remplaçant “célibataire” par “homme non marié”). En admettant que la notion de vérité logique soit suffisamment claire – Quine pensait l’avoir éclaircie in (1936) –, nous pourrions dire que nous avons rendu scientifiquement respectable la notion générale d’analyticité si nous parvenons à rendre claire la notion de synonymie. On peut penser le faire avec le concept de définition : on pourrait dire que “célibataire” est défini comme “homme non marié”. Mais qu’est-ce qu’une définition ? Il existe des définitions de dictionnaire, qui se contentent toutefois d’enregistrer certaines uniformités d’utilisation, et en réalité présupposent le concept de synonymie (le lexicographe définit “célibataire” par “homme non marié” parce qu’il pense que les deux expressions sont synonymes). Il y a ensuite les explications, qui ont pour but de substituer une expression vague du langage naturel (par exemple “probable”) par une expression scientifique précise et correspondant à la première au moins dans certains contextes d’utilisation significatifs : elles aussi présupposent la notion de synonymie, parce que l’explicans (l’expression précise) est proposé comme remplaçant l’explicandum (l’expression vague que l’on veut remplacer) en tant qu’il est (dans certains contextes) son synonyme. Il y a enfin les stipulations, qui introduisent dans un langage scientifique un terme nouveau sur la base de termes anciens (comme lorsqu’on dit, par exemple : « Appelons “ensemble puissance” de l’ensemble A l’ensemble des sous-ensembles de A »). Les stipulations constituent effectivement une synonymie, et ne la présupposent pas ; mais elles couvrent un nombre très limité de cas (ce n’est certainement pas par stipulation que “célibataire” est synonyme d’“homme non marié”).

La substituabilité est une alternative : deux expressions, pourrait-on dire, sont synonymes si et seulement si elles peuvent se substituer l’une à l’autre dans tous les contextes salva veritate, c’est-à-dire sans altérer la valeur de vérité des énoncés dans lesquels elles apparaissent. Mais cette proposition mérite d’être prise en considération uniquement si l’on précise que la formule « tous les contextes » inclut les contextes non extensionnels. Dans les contextes extensionnels, en effet, deux expressions peuvent se substituer l’une à l’autre sans être (intuitivement) synonymes. Par exemple, les deux prédicats “animal doté d’un cœur” et “animal doté de reins” peuvent se substituer l’un à l’autre dans les contextes extensionnels (parce que les deux prédicats ont, de fait, la même extension : tous les animaux dotés de cœur sont également doté de reins, et réciproquement), mais ne sont pas intuitivement synonymes. Par contre, la substituabilité fait défaut dans les contextes intensionnels : par exemple

(23) Nécessairement un animal doté de cœur est doté de cœur

est vrai, tandis que

(24) Nécessairement un animal doté de reins est doté de cœur

est faux (parce que c’est un fait contingent et non une nécessité, que les animaux dotés de reins ont un cœur). Nous pouvons donc définir la synonymie comme intersubstituabilité (salva veritate) dans tous les contextes, y compris ceux intensionnels : la référence à ces derniers est essentielle si l’on veut définir une notion de synonymie qui reflète nos intuitions. Toutefois – se demande alors Quine – sur quelle base avons-nous établi que (23) est vrai (ou que (24) ne l’est pas) ? Quelles sont les conditions de vérité d’un énoncé commandé par l’adverbe “Nécessairement” ? Il semble qu’un énoncé de la forme “Il est nécessaire que p” soit vrai si et seulement si p est analytique. En disant cela, Quine fait référence à l’analyse des concepts modaux de Carnap (1947 ; cf. § 14) ; plus tard, quand Kripke proposera son analyse en termes de mondes possibles (§ 17, 32), Quine interviendra dans la discussion pour contester la légitimité philosophique de tout l’appareil conceptuel de la théorie (pour une reconstruction de la discussion voir Linsky, 1971 : 1-16).

Ainsi tenter d’éclairer la notion d’analyticité, revient à entrer dans un cercle vicieux : l’analyticité est expliquée (dans le cas général) en terme de synonymie, la synonymie est définie en termes d’intersubstituabilité dans un langage intensionnel, mais la décision sur l’intersubstituabilité dans les contextes (intensionnels) de la forme “Il est nécessaire que p” dépend de la reconnaissance de l’analyticité de p. L’argumentation de Quine a été critiquée par plusieurs auteurs, mais, dans l’ensemble, elle s’est avérée persuasive, et a jeté un discrédit quasi définitif sur la vénérable distinction entre énoncés analytiques et énoncés synthétiques. Il faut dire que Quine lui-même a précisé (par exemple in 1960 : 289) qu’il n’avait pas eu l’intention de contester « nos indéniables intuitions de synonymie et d’analyticité ». Quine n’a pas voulu dire qu’il n’y avait aucune différence, quant aux raisons de vérité, entre “Aucun célibataire est marié” et “Napoléon est mort en 1821”. Il a voulu dire que la notion de signification théorisée, ou implicitement présupposée, tant par les néo-positivistes comme Carnap que par les « analystes du langage » oxfordiens comme Austin (Quine ne s’intéressa d’ailleurs à cette école que très incidemment) est insoutenable. Elle se fonde sur la possibilité d’identifier certaines informations comme pertinentes pour la signification d’un mot (contrairement à d’autres, qui seraient « simplement factuelles ») ; c’est-à-dire sur la possibilité de faire une distinction systématique entre énoncés analytiques (“Les chats sont des animaux”) et des énoncés synthétiques (“Tous les chats de mon quartier sont sales”). Nos « indéniables intuitions » de synonymie et d’analyticité ne soutiennent pas, selon Quine, une telle distinction systématique. Elles soutiennent seulement une gradation entre les informations et les énoncés qui les expriment. Toutes les vérités sont telles, tant en vertu du langage que par la force des faits (si “Napoléon” désignait Jules César, “Napoléon est mort en 1821” serait faux) ; mais pour certaines, les faits semblent moins importants que pour d’autres. Ou, pour être plus précis, il y a des vérités – comme celles de la logique et de la mathématique – que nous serions extrêmement réticents à abandonner indépendamment de l’état des choses, et d’autres (comme celle portant sur les chats de mon quartier) auxquelles les faits nous feraient facilement renoncer. Quine était parvenu à cette conception il y a déjà de nombreuses années, dans Vérité par convention (1936) : en refusant la fondation conventionaliste de la logique, il reconduisait la dichotomie entre vérités a priori (comme celles de la logique) et vérités a posteriori à une « opposition entre des assertions acceptées avec une plus ou moins grande fermeté... Il y a des assertions que nous décidons d’abandonner en dernier recours, si nous sommes vraiment obligés de le faire, dans le cours du rapiéçage de nos sciences à la lumière de nouvelles découvertes ; et parmi elles, il y en a que nous n’abandonnerons jamais, tant elles sont fondamentales pour tout notre schéma conceptuel. Parmi ces dernières il faut compter les vérités logiques et mathématiques » (1936 : 166).

Tombe ainsi, sous le feu de la critique de Quine, le programme de l’« analyse du langage », dans la mesure où il présupposait une démarcation rigide entre conceptuel et factuel ; tombe par conséquent également l’idée d’une nette séparation entre philosophie (consacrée à des analyses conceptuelles) et science (consacrée à des recherches factuelles) – séparation sur laquelle avait grandement insisté Wittgenstein, jusqu’à ses dernières années. Et tombe, surtout, une forme de la distinction entre langage et théorie : à l’intérieur d’un langage (entendu comme ensemble d’énoncés syntaxiques bien constitués) on peut distinguer les énoncés vrais des énoncés faux, mais on ne peut pas distinguer les énoncés constitutifs des significations des mots (“Les chats sont des animaux”) des énoncés, disons, applicatifs des significations des mots (“Les chats de l’île de Man ont la queue coupée”). On ouvre ainsi la porte, entre autres, à ladite thèse de l’incommensurabilité des théories, qui présuppose l’importance sémantique de toutes les assertions d’une théorie (holisme sémantique). Et nous verrons (§ 30) comment Davidson portera la critique de Quine à ses extrêmes conséquences, en niant une distinction à laquelle Quine était resté attaché : celle entre schéma conceptuel et contenu d’une théorie.

28. Indétermination de la signification et de la référence.

On peut penser déterminer la signification d’une expression linguistique en spécifiant les connexions intralinguistiques qui la constituent, c’est-à-dire en inventoriant les énoncés analytiques dans lesquels l’expression apparaît (on peut penser définir “chat” en spécifiant que les énoncés suivants sont analytiques : “les chats sont des animaux”, “les chats sont des félins”, “les chats sont domestiques”, etc.). La critique de Quine concernant la distinction analytique/synthétique, si elle est efficace, montre que cette voie n’est pas praticable. On peut, comme alternative, penser déterminer la signification d’une expression à travers ses connexions avec la réalité extra-linguistique, c’est-à-dire – si l’on est empiriste – avec l’expérience. La signification d’un mot comme “jaune” est donnée par son lien avec l’expérience de la couleur jaune ; la signification d’un énoncé coïncide avec le mode de sa confirmation empirique. Comme on l’a déjà vu (§ 12), ce projet – d’une réduction des significations à l’expérience sensible – faisait partie du programme du premier néo-positivisme : dans Deux dogmes (1951 : 115), Quine avait critiqué l’application qu’en avait faite Carnap dans (1928), en montrant que la réduction proposée était (et ne pouvait qu’être) incomplète. Les deux idées de la distinction analytique/synthétique et de la réductibilité des significations à une base purement empirique – les « deux dogmes » de l’empirisme – ont, pour Quine, une racine commune : la thèse selon laquelle la vérité d’un énoncé est déterminée par deux facteurs distincts, l’un linguistique et l’autre factuel et empirique (1951 : 116). Ou plutôt, ce qui rapproche les deux dogmes, c’est l’idée que les significations des expressions d’un langage sont spécifiables une par une, à travers ces connexions linguistiques ou extra-linguistiques.

Dans Le mot et la chose (1960), Quine essaye de prendre au sérieux l’idée d’un fondement empirique des significations. Il imagine une situation dans laquelle il faut interpréter un langage – dans l’expérience de pensée de Quine, de le traduire dans sa propre langue – uniquement sur la base du comportement (linguistique et non linguistique) de celui qui le parle, et des données perceptives que l’on suppose également disponibles aux locuteurs et à l’interprète. C’est la situation de la traduction radicale : une traduction entre deux langues qui n’ont pas de canaux culturels de communication, parce qu’elles appartiennent à des cultures que l’on suppose complètement séparées. Il s’agit d’une situation dans laquelle l’assignation de signification aux expressions d’un langage n’a pas d’autre base que les connexions du langage avec l’expérience, telles qu’elles apparaissent accessibles pour un observateur. Dans une telle situation, dit Quine, la traduction serait indéterminée : on pourrait concevoir différents manuels de traduction, incompatibles entre eux et pourtant également compatibles avec toutes les données disponibles, c’est-à-dire avec tous les comportements linguistiques et non linguistiques des locuteurs et avec toutes les données perceptives disponibles au traducteur (pour un exposé synthétique mais complet de l’argumentation de Quine, voir Casalegno, 1997 : chap. 9). Par exemple, un manuel de traduction pourrait traduire le mot étranger “gavavai” par “lapin”, un autre par “partie non séparée de lapin”, et un autre encore par “stade temporaire de lapin” ; et il n’existe pas de « faits » – données perceptives, comportements linguistiques, geste d’ostension ou autre – susceptibles de décider, entre les différents manuels, lequel est « juste ». Parce que les trois traductions sont équivalentes du point de vue de la perception, et correspondent à la même « portion de monde » perceptive : « La seule différence – dit Quine – tient à la manière dont on découpe [le monde], et c’est une chose que ni l’ostension ni le simple conditionnement ne peuvent montrer ». Il peut sembler, dit encore Quine (1960 : 92), que l’incertitude de la traduction puisse être éliminée par quelque question supplémentaire au natif, et quelque geste ostensif en plus. Mais réfléchissons sur la manière dont cela pourrait se passer. « Indiquez un lapin, et vous aurez indiqué un état temporaire de lapin, une partie non séparée du lapin, une exemplification de la lapinité, etc. Rien qui ne soit distinct en terme de stimulations ne peut être distingué par l’ostension, à moins que l’ostension soit accompagnée de questions telles que : “Est-ce le même gavavai que celui-là ?”, “Y a-t-il ici un ou deux gavavai ?”, et cætera » (Ibidem). Mais ces questions ne sont possibles que si nous avons identifié la structure du langage étranger, c’est-à-dire si nous avons compris quels instruments linguistiques ont comme fonctions des fonctions semblables à celles qu’ont dans notre langue les articles, les pronoms, le singulier et le pluriel, la copule, le prédicat d’identité, etc. La structure est idiosyncratique à une langue, et la correspondance entre des structures interagit avec la correspondance entre des unités lexicales (“gavavai” et “lapin”) : dans un certain contexte perceptif, “gavavai” peut être traduit par “partie de lapin” (plutôt que “lapin”), en adaptant opportunément la traduction d’aspects structuraux – par exemple en traduisant une certaine expression étrangère par “est une partie de” au lieu de “est identique à”.

Ce qui intéresse Quine ce n’est pas la traduction, mais la signification : il entend soutenir que la signification et la référence des expressions d’un langage ne peuvent pas être déterminées sur la seule base du comportement linguistique des locuteurs en relation à des données perceptives présumées communes aux locuteurs et à l’interprète. En disant que “lapin” se réfère aux lapins – il ne s’agit donc plus ici de traduction – nous laissons toujours ouverte la porte à la question : « En quel sens de “lapin” ? » (1969 : 62). Et indiquer un ou plusieurs lapins ne sert à rien, du fait de l’indétermination de l’ostension. Le problème n’est pas le caractère vague du geste d’ostension (il se peut qu’il ne soit pas clair que nous indiquons l’oreille du lapin ou le lapin tout entier), mais le fait qu’un geste d’ostension ne puisse expliciter la conceptualisation qu’il présuppose : le stimulus perceptif qui est indiqué peut être conceptualisé de différentes manières. La détermination est possible, selon Quine, uniquement à partir d’une « théorie d’arrière-plan » : des attributions de signification et référence aux expressions d’un langage ne sont possibles que dans un autre langage, que l’on suppose interprété et partagé. Ce langage interprété et partagé donne un sens déterminé à la question : « En quel sens de “lapin” ? » : il fournit un cadre linguistique dans lequel la question peut avoir une réponse. Une attribution déterminée de signification n’est possible que comme traduction en un langage interprété et partagé. Il n’y a pas d’interprétation comme mise en correspondance directe entre langage et monde (comme le pensaient certains néo-positivistes) : une attribution de signification est toujours relative à un langage interprété. Une attribution absolue de significations ou de références, dit Quine, est dénuée de sens : « Ce qui a un sens c’est de dire comment une théorie d’objets est interprétable ou réinterprétable dans une autre et point de vouloir dire ce que sont les objets d’une théorie, absolument parlant » (1969 : 63). En dernière analyse il n’y a pas d’attributions de significations, il n’y a que des traductions.

29. Embrigader le langage naturel.

Il résulte des analyses de Quine que toute attribution de signification est relative à une théorie d’arrière-plan. De fait, la théorie qui sert d’arrière-plan aux langages spécialisés des sciences, et à n’importe quel autre système sémantique qui puisse nous venir à l’esprit, n’est autre que le langage naturel. La reconnaissance du primat du langage naturel (qui n’est pas de principe, mais de fait) n’implique pas toutefois, dans le cas de Quine, qu’il soit traité comme « sacro-saint » (1960 : 28), comme pourrait le faire un herméneute ou un disciple d’Austin. Au contraire, le langage naturel doit, et en même temps demande à être « embrigadé » (regimented), pour être libéré des « anomalies et conflits qui tendent à empêcher la communication, estropier la déduction, rendre obscurs les engagements ontiques et perturber la construction des théories » (Gibson, 1982 : 145). « Les raisons qui déterminent les hommes de science à chercher des théories toujours plus simples et claires [...] sont aussi les raisons qui nous poussent à simplifier et à clarifier la structure plus ample qui est commune à toutes les sciences » (Quine, 1960 : 232). En embrigadant le langage naturel, l’étoile du berger de Quine c’est le langage de la logique élémentaire (substantiellement, le langage prédicatif de premier ordre avec identité). Pour Quine, il possède des qualités exemplaires de clarté, d’économie, de transparence ontologique ; le langage naturel doit être autant que possible reconduit au langage de la logique. Il ne doit pas être remplacé par un langage symbolique, mais il s’agit plutôt de retrouver dans le langage naturel lui-même, du mieux que l’on peut, cette structure logique que le langage symbolique exhibe avec une pleine évidence, et dont les éléments constitutifs sont la prédication, la quantification, les fonctions de vérité, les variables et les termes généraux. Il s’agit donc de faire voir, avant toute chose, que des expressions ou des constructions naturelles apparemment non reconductibles à des formes de premier ordre peuvent être paraphrasées par des expressions toujours naturelles, même si elles sont moins élégantes, qui sont – plus ou moins – équivalentes à celles de départ et exhibent pourtant de manière plus transparente une structure philosophiquement et logiquement acceptable. Quine appelle ces paraphrases : formes canoniques. C’est la procédure que Russell (§ 9) avait appliquée aux descriptions (selon laquelle par exemple, “Un homme pense” est paraphrasé par “Il y a un x tel que x est un homme et x pense”) et déjà Frege avait développé la théorie de la quantification en montrant par exemple que “Tous les P sont Q” peut être paraphrasé par “Pour chaque x, si x est P alors x est Q”. Par cet aspect de sa proposition, Quine appartient pleinement à la tradition de Russell et du Tractatus logico-philosophicus, dans laquelle on fait la distinction entre « forme apparente » (superficielle, grammaticale) et « forme réelle » (profonde, logique) des expressions du langage naturel, et l’on assigne à l’analyse philosophique la tâche de révéler la forme logique « sous » la forme grammaticale superficielle. Certes, la paraphrase en forme canonique peut impliquer quelque violence faite au lagage tel qu’il est ; mais Quine ne conçoit pas sa tâche comme celle d’un linguiste qui veut décrire la structure sémantique du langage naturel, mais au contraire comme celle d’un philosophe qui veut améliorer un instrument – le langage naturel – indispensable pour le travail scientifique.

Dans certains cas, le langage naturel ne peut être débarrassé de l’obscurité grâce à la paraphrase en forme canonique : il y a des choses que le langage nous laisse dire, et que nous devrions simplement éviter de dire. Comme jadis Frege, Quine n’est pas hostile à des attitudes éliminatives à l’égard du langage naturel. L’exemple principal est donné par certaines utilisations du langage modal, comme celles où l’adverbe “nécessairement” est utilisé de re (« Un mathématicien est nécessairement rationnel »). Ces utilisations portent en elles d’inextricables embrouillaminis métaphysiques et induisent à supposer des entités peu plausibles (comme les essences) ; ils devraient être simplement évités. On voit ainsi comment Quine n’hésite pas à invoquer des considérations strictement philosophiques – comme la plausibilité intrinsèque d’une ontologie – comme critère pour embrigader le langage naturel. Par cet aspect, il est un héritier de la philosophie linguistique (§ 2), et son travail appartient à la métaphysique (analytique) plus qu’à la philosophie du langage.

30. Davidson.

À partir d’un article paru en 1967, Vérité et signification, Donald Davidson (né en 1917) a proposé une idée de la théorie sémantique fondée sur la théorie de la vérité de Tarski (§ 13), et il l’a défendue en utilisant de manière originale des concepts élaborés par Quine dans Le mot et la chose (§ 28). Pour Davidson, comme pour le paradigme dominant, donner les conditions nécessaires et suffisantes pour la vérité d’un énoncé c’est une manière d’en donner la signification (1967 : 51) : « Savoir ce qu’est pour un énoncé [d’un langage] être vrai [...] équivaut à [...] comprendre le langage » (Ibidem), c’est-à-dire à connaître la signification de ses énoncés. Expliciter les conditions de vérité des énoncés d’un langage L, c’est formuler une théorie de la vérité pour L : où par “théorie de la vérité”, on entend un ensemble d’axiomes qui implique, pour chaque énoncé du langage, une énonciation des conditions auxquelles celui-ci est vrai (1970 : 94). Or, c’est précisément ce qui fait une définition de vérité au sens de Tarski : comme nous le savons, une telle définition, si elle est adéquate, rend déductibles tous les biconditionnels de la forme

(T) S est vrai (en L) si et seulement si p,

où “S” est le nom d’un énoncé de L et p est sa traduction dans le métalangage dans lequel la définition est formulée. Donc une définition de vérité tarskienne est automatiquement une théorie de la signification, mais à condition qu’elle soit interprétée différemment de la manière dont l’interprète Tarski. Disons que pour ce dernier, les axiomes de la théorie sont des hypothèses sur la signification du prédicat “vrai” en tant qu’il est appliqué à des énoncés de L : les hypothèses sont validées si l’on parvient à démontrer qu’à partir des axiomes sont déductibles tous les biconditionnels de la forme (T). En effet, Tarski présuppose que les T-biconditionnels saisissent le noyau de notre concept de vérité, c’est pourquoi une théorie à partir de laquelle ils sont dérivables est une définition adéquate de vérité (pour L). À son tour, cela présuppose que les biconditionnels soient des énoncés signifiants, et que leurs côtés droits soient effectivement la traduction métalinguistique des côtés gauches : sans quoi on ne pourrait affirmer qu’ils saisissent nos intuitions sur la vérité (voir Marconi, 1984 : 89).

Du point de vue de Davidson, au contraire, les axiomes de la théorie doivent être entendus comme des hypothèses sur la signification des expressions de base du langage dont on veut donner la sémantique : elles sont validées si les biconditionnels qui en sont déduits expriment effectivement les conditions de vérité des énoncés de L. Ce qui présuppose que le métalangage dans lequel la théorie est formulée soit compris, et que l’on sache ce que veut dire “vrai” : c’est à cette seule condition qu’il est possible de confirmer ou d’infirmer la théorie, en vérifiant si effectivement les côtés gauches des biconditionnels sont vrais exactement quand les côtés droits correspondants (que nous comprenons) sont également valables. Chez Tarski, on sait déjà que les biconditionnels sont vrais (la question est de savoir si on parvient à les déduire des axiomes de la théorie) ; chez Davidson, il s’agit d’établir s’ils le sont : une théorie de la vérité interprétée comme théorie de la signification pour une langue naturelle est une théorie empirique (1973 : 199-200). Supposons qu’une théorie de la vérité pour l’anglais ait entre autres pour conséquences

“It rains” est vrai (en anglais) si, et seulement si, il fait froid.

Dans la mesure où nous comprenons le métalangage (y compris l’énoncé “il fait froid”) et que nous savons ce que veut dire “est vrai”, nous sommes capables d’établir que la théorie est fausse : l’énoncé anglais “it rains” n’est nullement vrai si, et seulement si, il fait froid.

Comment y parvient-on ? Ici intervient l’appareil conceptuel quinien. D’après Davidson, la construction d’une théorie de la vérité (entendue comme théorie sémantique) pour un langage doit être conçue comme une tentative d’interprétation radicale : à savoir mettre à disposition d’un interprète toutes les informations dont il a besoin pour comprendre une langue qu’initialement il ne comprend pas du tout. La construction de la théorie doit se fonder uniquement sur les manifestations de consentement et de non-consentement des locuteurs étrangers (on suppose que l’interprète est en mesure de reconnaître quand un locuteur étranger manifeste qu’il considère comme vrai un énoncé dans des circonstances déterminées), et sur des faits, que l’on suppose également accessibles au locuteur et à l’interprète (1973 : 203 et n.). Ainsi, par exemple, nous pourrions parvenir à établir qu’un locuteur anglais montre qu’il considère vrai “it rains” non pas dans tous les cas où il fait froid et seulement dans ces cas, mais dans tous les cas où il pleut et seulement dans ces cas. Naturellement, le locuteur auquel nous avons affaire pourrait se tromper ou mentir ; d’autre part, du moins au début, nous n’avons pas d’autre choix que de le considérer comme crédible (c’est-à-dire maximiser l’accord entre le locuteur et nous, quant au jugement sur les circonstances de fait en relation auxquelles nous interprétons le langage). C’est l’assomption du principe de charité de Quine.

Il y a une objection immédiate à la méthode de l’interprétation radicale, et en réalité à l’assomption d’une théorie de la vérité tarskienne comme théorie de la signification. Les T-biconditionnels ne sanctionnent qu’une identité extensionnelle entre les côtes droits et les côtés gauches, et non une identité de signification. Par exemple, le biconditionnel

“Grass is green” est vrai (en anglais) si et seulement si la neige est blanche

est vrai, mais “grass is green” ne signifie pas « la neige est blanche » : simplement il advient que les deux énoncés sont vrais. Davidson considère que l’objection peut être dépassée si l’on adopte un point de vue holiste : en considérant ensemble tous les T-biconditionnels pour les énoncés du langage « nous connaîtrons le rôle que joue chaque partie significative de l’énoncé, et [...] les connexions logiques entre cet énoncé et d’autres » (1973 : 206 ; voir Engel, 1994 : 50-53). Par exemple, nous connaîtrons le rôle de “grass” dans plusieurs énoncés, et nous serons en mesure d’exclure qu’il puisse signifier « neige ». Il faut noter que dans ce cas, “holiste” signifie uniquement « non atomique » : il n’est pas clair que pour palier à l’inconvénient dont nous avons parlé supra, nous devions prendre en considération tous les biconditionnels (et d’autre part, Davidson ne démontre pas qu’en les prenant tous en considération le problème soit résolu : il ne fait dans ce cas qu’une conjecture raisonnable).

Comme la traduction radicale pour Quine, l’interprétation radicale de Davidson est une expérience de pensée, qui devrait montrer sur quoi se fonde l’interprétation sémantique d’un langage (essentiellement, sur des jugements de vérité des locuteurs dans des circonstances de faits déterminées). Quine avait déduit de l’analyse de la traduction radicale l’indétermination de la signification. Davidson ne la nie pas, mais la dédramatise : chaque théorie de la vérité empiriquement confirmée constitue une interprétation du langage, même s’il sera possible d’en construire d’autres, également confirmées, qui articulent différemment les rapports entre les significations et les croyances (1973 : 206).

En effet, chaque divergence entre nos jugements de vérité et ceux d’un autre locuteur peut toujours être reconduite soit à des croyances différentes, soit au fait qu’aux mêmes mots nous attribuons des significations différentes. Rien ne peut nous obliger à un choix plutôt qu’à un autre. Donc, la distinction entre schéma conceptuel et contenu, que Quine accepte également, est infondée pour Davidson, dans le sens où il n’existe pas de traits du comportement linguistique d’un locuteur qui doivent être reconduits à son schéma conceptuel (c’est-à-dire aux significations selon lesquelles il utilise les mots) plutôt qu’au contenu de ses croyances, ou réciproquement (Davidson, 1974).

Plus récemment (1986), Davidson a soutenu que l’interprétation est une opération que chaque locuteur accomplit à l’égard de chaque autre locuteur au cours de chaque interaction linguistique, et ce sont également les limites de sa validité : on ne devrait pas donner pour acquis (comme il l’avait fait, voir par ex. 1973 : 201) qu’elle s’applique à une langue, partagée par une communauté linguistique. La langue dont ont parlé les philosophes – un système de conventions appris et partagé – n’existe pas : et ni la théorie interprétative avec laquelle un interprète se prépare à l’interaction avec un locuteur déterminé (théorie antécédente), ni celle qui résulte de l’adaptation de la théorie antécédente au comportement linguistique effectif du locuteur (théorie transitoire) ne sont partagées par une communauté. La capacité de communiquer ne consiste que dans la capacité de comprendre et de se faire comprendre (1986 : 173) : le processus de formation d’une « théorie transitoire » ne peut pas plus être soumis à des règles que ne peut l’être le processus de création d’une nouvelle théorie devant rendre compte de nouvelles données, dans quelque domaine que ce soit.

31. Le démantèlement du paradigme dominant.

À partir du début des années soixante-dix, le paradigme frégéen fut soumis à différentes critiques (et même, au moins à première vue, contradictoires), qui eurent pour effet de miner sa crédibilité globale, sans pour autant donner lieu à un paradigme alternatif. Les réflexions de Kripke et de Putnam sur la valeur sémantique des noms propres (comme “Napoléon” ou ”France”) et des noms de substance et espèce naturelles (comme “or” ou “citron”) mettent en discussion la validité générale des analyses fondées sur les concepts de sens et de dénotation (Frege), ou extension et intension (Carnap, Montague). Émerge un point de vue qui tend à identifier sans résidus la signification avec la dénotation ou référence (théorie de la référence directe), en montrant – comme l’avait déjà fait Russell (§ 9) – que des notions comme celle de sens ne peuvent être tenues comme pertinentes pour la détermination des conditions de vérités des énoncés.

Parallèlement, la réflexion sur le langage qui se développe dans le cadre de la psychologie cognitive et de l’Intelligence Artificielle (I.A.) tend au contraire à revendiquer la pertinence, pour la théorie sémantique, des processus d’élaboration du langage imputables à un esprit fini, naturel ou artificiel (et donc la thèse 3 du paradigme dominant – voir § 4 – est contestée). La sémantique traditionnelle est souvent jugée incapable de servir de base à une théorie de la compréhension du langage ; par conséquent, son droit à l’appellation de “sémantique” – théorie de la signification – est également mis en doute, étant donné le lien toujours plus étroit qui est reconnu entre signification et compréhension. La philosophie du langage accepte toujours plus de se faire suggérer des thèmes et des solutions par les sciences cognitives : dans le cours des années quatre-vingt, on assiste à une substitution graduelle du modèle reconnu de la logique – et sur l’efficacité duquel, de Frege à Montague, nous avons insisté – par un modèle que nous pourrions appeler computationnel. Alors que pour le paradigme dominant, il s’agissait de représenter les relations sémantiques sur le modèle des relations inférentielles dans un système de logique, la sémantique d’orientation cognitive se propose de représenter la compréhension du langage comme un calcul exécuté par un système (naturel ou artificiel), dont les caractéristiques sont conçues à partir de la science des ordinateurs (et la logique retrouve ici son rôle, voir Lolli, 1991 ; Frixione, 1994).

Certes, même au cours de ces années, de nombreux chercheurs continuent de partager pour l’essentiel le point de vue de Frege, ou d’analyser le langage dans le cadre de la grammaire de Montague ou d’autres théories formelles analogues ; et des tentatives de « réforme » du paradigme, essayant de remédier à son inadéquation descriptive là où elle est la plus évidente, sont explorées (§ 35). Mais le paradigme dominant est jugé toujours plus souvent soit trop cognitif ou contaminé par le mentalisme (par les théoriciens de la référence directe), soit au contraire trop peu cognitif (par les sémanticiens cognitifs). Une tentative de synthèse entre ces instances opposées est proposée par les « théories duelles » (§ 34) ; mais ces propositions semblent – pour le moment – fragiles et incapables de résoudre la dichotomie entre référentialisme pur et cognitivisme. Au début des années quatre-vingt-dix, la théorie des conditions de vérité et la théorie de la compréhension semblent constituer, pour la sémantique, deux voies différentes et alternatives.

32. Théorie de la référence directe.

Au cours des années soixante-dix, et de manière plus affirmée dans la décennie suivante, on fut de plus en plus convaincu que Frege avait chargé le concept de sens de deux fonctions différentes : d’un côté, le sens d’une expression est ce qui en détermine la dénotation ou référence ; de l’autre, le sens est une entité cognitive, qui hérite de la fonction de la notion traditionnelle de concept ; par exemple, le sens d’une expression est ce qu’un locuteur compétent connaît, du fait qu’il comprend cette expression. Mais, au moins dans certains cas et peut-être dans tous, les deux fonctions sont incompatibles : ce qui détermine la référence n’est pas un contenu possible de la compétence sémantique, et d’autre part ce qu’un locuteur associe à une expression n’est pas ce qui en détermine la référence. La dissociation des deux fonctions est argumentée initialement par Kripke pour le cas des noms propres, avant d’être étendue à d’autres catégories d’expressions.

Dans une sémantique des mondes possibles, à la manière de Kripke (§ 17), si un énoncé d’identité de la forme a = b est vrai, il est aussi nécessairement vrai. C’est le cas parce que, dans ces sémantiques, chaque interprétation assigne à une constante individuelle le même individu dans tous les mondes possibles ; ainsi, si l’on associe le même individu dans le monde réel à “a” et “b” (dès lors que “a = b” est vrai), il leur sera associé également un même individu dans tous les mondes possibles : donc l’identité “a = b” vaut dans tous les mondes possibles, ce qui revient à dire qu’elle est une identité nécessaire. En rappelant que les constantes individuelles tiennent, dans un langage formel, le rôle des noms propres, il est facile de comprendre comment cette conséquence pourrait sembler contre-intuitive : comment une identité comme « Hespéros = Phosphoros » peut-elle être nécessaire  ? Il est facile d’imaginer un monde possible dans lequel l’étoile qui apparaît la première le soir (Hespéros) et celle qui disparaît la dernière le matin (Phosphoros) sont deux corps célestes différents. Dans une série de conférences tenues en 1970, parues sous le titre Nom et nécessité [La logique des noms propres] en 1972, Kripke répliqua en soutenant la pleine légitimité de la thèse contestée, également en relation au langage naturel : les identités qui impliquent des noms propres (comme “Hespéros = Phosphoros”) sont effectivement nécessaires, parce qu’un nom propre dénote le même individu dans tous les mondes possibles (c’est un désignateur rigide). La position du paradigme dominant était, à cet égard, différente. Ce qu’un nom propre dénote est déterminé par son sens ; si l’on considère – comme le pensait probablement Frege – que le sens du nom est exprimé par une description définie (par exemple “l’étoile du soir” dans le cas d’“Hespéros”) alors il est possible que, dans des mondes différents, des objets différents satisfassent la description, et que donc le nom dénote des objets différents. Cela vaut également si l’on pense, comme Russell, que les noms propres normaux sont des descriptions définies « masquées » (§ 9) : ce sera en tout cas la description qui déterminera la dénotation du nom propre.

Contre le paradigme, Kripke soutient que les noms propres ne sont nullement des synonymes de descriptions, ni au sens de Frege ni au sens de Russell ; en vérité, les noms propres n’ont pas de sens : leur valeur sémantique consiste (entièrement) dans leur référence. On a habituellement subdivisé les arguments de Kripke contre la théorie traditionnelle en trois groupes : épistémologiques, métaphysiques, sémantiques. Les arguments sémantiques sont peut-être les plus immédiats. Par exemple : « Si “Aristote” signifiait l’homme qui fut le maître d’Alexandre le Grand, alors dire “Aristote fut le maître d’Alexandre le Grand” serait une simple tautologie. Mais il est clair que ce n’est pas le cas : cela exprime le fait [je souligne] qu’Aristote fut le maître d’Alexandre le Grand » (1972 : 45). Voici par contre, un exemple d’argument épistémologique. Disons que le nom propre “Kurt Gödel” soit considéré comme le synonyme de “celui qui a découvert le théorème d’incomplétude de l’arithmétique”. C’est très certainement la seule information qui soit associée par une majorité d’individus au nom de “Gödel”. Si nous découvrions qu’en fait ce théorème fut conçu par un certain Schmidt (auquel, dans sa grande malhonnêteté, Gödel subtilisa les notes), dirons-nous que le nom ”Gödel” se réfère en réalité à Schmidt ? Non pas ; nous dirons justement que celui qui a découvert le théorème n’est pas Gödel mais Schmidt (1972 : 78-79).

Les arguments métaphysiques sont fondés sur nos intuitions modales, relatives à ce qui est possible ou non. Disons que “Aristote” soit considéré comme synonyme du “philosophe né à Stagire, auteur de la Métaphysique”. Il s’ensuit que l’énoncé “Aristote naquit à Stagire et écrivit la Métaphysique”, étant analytique, est également nécessaire. C’est-à-dire qu’il est nécessaire qu’Aristote soit né à Stagire, etc. Ce qui – bien évidemment – n’est pas le cas : Aristote aurait pu naître ailleurs, et c’est un fait contingent qu’il soit né précisément à Stagire ; de même qu’il aurait pu mourir à trois mois et ne pas composer la Métaphysique. Nos intuitions nous disent qu’aucun énoncé du type «Aristote = “le ceci ou cela” n’est nécessaire. Il en va de même si un nom est considéré comme équivalent à une disjonction de descriptions, comme l’avait soutenu Searle (1958 ; 1969 : 223) et Wittgenstein avant lui (1953 : § 79) : par exemple “le philosophe né à Stagire ou l’auteur de la Métaphysique ou le maître d’Alexandre le Grand, ou ...” : parce qu’Aristote – cet individu-là – aurait pu ne rien faire de tout cela.

Une objection évidente à Kripke est qu’il semble qu’il y ait des cas où la synonymie entre un nom et une description est forcée : par exemple, lorsqu’un nom est introduit dans le langage à travers une description. Celui qui introduit le nom “Hespéros” pour la planète Vénus aurait pu dire : j’utiliserai “Hespéros” comme nom du corps céleste qui apparaît à tel endroit dans le ciel. Dans ce cas, “Hespéros” n’est-il pas synonyme de “le corps céleste etc.” ? Non, dit Kripke ; la description est certes utilisée pour fixer la référence du nom, mais elle n’en donne pas la signification. « Si Hespéros avait heurté précédemment une comète, il aurait pu être visible à une position différente [...] Dans une situation contrefactuelle de ce genre, nous dirions que Hespéros n’aurait pas occupé cette position, mais non pas que Hespéros n’aurait pas été Hespéros » (1972 : 90).

À la place de la théorie traditionnelle, Kripke propose une image alternative de la manière dont un nom propre en vient à se trouver doté de la référence par laquelle il est utilisé dans le langage. Un nom acquiert initialement sa propre référence grâce à un baptême : un « rite » dans lequel le nom est directement associé à son référent, qui est physiquement présent. Cette association initiale se transmet de locuteur à locuteur sur la base d’une relation, accompagnée de l’intention (caractéristique d’une communauté linguistique) que chaque locuteur a d’utiliser le nom tel qu’il est utilisé par les locuteurs qui lui en enseignent l’utilisation. Cette « chaîne » d’utilisations du nom est nommée par Kripke chaîne causale, parce que la référence est transmise par des relations causales (comme la relation d’apprendre par un locuteur la manière dont un nom est utilisé). On a observé (Evans, 1973 : 202) que malgré les intentions des locuteurs, la chaîne causale de Kripke ne transmet pas toujours la référence instituée par le baptême initial : par exemple le nom “Madagascar” désignait à l’origine une partie de la côte africaine, et par la suite, du fait d’une méprise de Marco Polo, il en vint à désigner la grande île qui lui faisait face. Si c’est le baptême qui compte, “Madagascar” devrait aujourd’hui encore désigner cette partie de la côte africaine (ce qui n’est pas le cas). Plus généralement, on a observé (Napoli, 1992 : 388) que La Logique des noms propres répond à deux questions distinctes : (a) en quoi consiste la valeur sémantique des noms propres ? et (b) de quelle manière les noms propres en viennent à avoir leur valeur sémantique ? La réponse à la seconde question – l’image du baptême et de la chaîne causale – est moins convaincante (Kripke lui-même en est conscient, 1972 : 81) que celle apportée à la première, qui est que la valeur sémantique des noms propres consiste exclusivement dans leur référence. Dans la mesure où l’idée centrale de Kripke est que la référence d’un nom lui est associée directement, sans la médiation d’un sens frégéen, on parle à cet égard de théorie de la référence directe des noms propres (sur cette théorie en général, voir, Récanati, 1993 : chap. 8).

Des considérations analogues furent développées par Kripke lui-même (1972 : 125 q.) et par Hilary Putnam (né en 1926) à propos des noms d’espèce et de substance naturelle. La référence de mots comme “eau” ou “tigre” n’est pas déterminée par un ensemble de conditions associées au mot lui-même (par exemple pour “eau”, qu’il s’agisse d’un liquide incolore, sans saveur particulière, qui bout à 100°, qui gèle à 4°, etc.) qui en constituent la définition ; quelque chose pourrait ne pas satisfaire la définition et être également de l’eau (et donc faire partie de la référence du mot “eau”). Putnam ne fait pas seulement allusion au fait que les définitions usuelles du dictionnaire ne déterminent pas vraiment l’extension des mots définis (par exemple le fait que les tigres aient un pelage à rayures jaunes et noires fait partie d’une définition normale du mot “tigre”, mais un tigre albinos n’en est pas moins tigre). Ceci vaut également pour la plus soignée des définitions que la science est en mesure de produire à un moment donné de son développement, et en général pour n’importe quelle détermination conceptuelle qu’un locuteur puisse avoir « en tête », en association à un nom d’espèce ou de substance naturelle. Pour faire voir que les sens – s’il s’agit de concepts ou d’entités mentales – ne déterminent pas la référence de ces mots, Putnam (1975 : 223-227 ; 1984 : 29-32) conçoit une ingénieuse expérience de pensée. Supposons qu’il existe une planète, Terre Jumelle, identique à la Terre si ce n’est que ses fleuves, ses lacs et ses mers sont pleins d’un liquide apparemment semblable à l’eau, mais dont la composition chimique est tout à fait différente et très complexe (dont l’abréviation serait XYZ). Dans le français parlé sur la planète Terre Jumelle ce liquide s’appelle “eau”. Sur Terre Jumelle, la chimie est aussi développée que sur Terre ; c’est pourquoi un terrejumellien qui visiterait aujourd’hui notre planète n’aurait aucune difficulté à reconnaître que, malgré les apparences, les deux liquides sont différents et n’appellerait pas “eau” (en terrejumellien) le liquide terrestre. Mais avant la naissance de la chimie – disons avant 1750 – aucun terrien ni terrejumellien n’aurait été en mesure de distinguer les deux liquides : un locuteur terrien, appelons-le Oscar_T, et son double terrejumellien Oscar_TJ auraient eu « en tête » exactement le même concept en association avec le mot “eau”. Et pourtant “eau” utilisé par Oscar_T, se réfère au liquide terrestre (H₂O)et non également à XYZ, tandis que “eau” utilisé par Oscar_TJ se réfère à XYZ et non également à H₂O. Si nous partageons ces intuitions de Putnam, nous reconnaîtrons que la référence du mot “eau” n’est pas déterminée par le sens associé au mot, mais par le fait d’avoir la même nature que le liquide en relation auquel le mot est utilisé paradigmatiquement ; un « fait » que le Putnam « réaliste métaphysique » des années soixante-dix considère comme déterminé tout à fait indépendamment de nos théories. En ce sens, une communauté linguistique tout entière et pas seulement un simple individu peut être dans l’erreur quant à la référence de “eau”, “or” ou “citron” : parce que les théories sur la base desquelles ces mots sont de fait appliqués peuvent attribuer par erreur la même nature à des objets (des échantillons de liquide par exemple) qui n’ont pas en réalité la même nature, ou ne pas l’attribuer à des objets qui l’ont.

Putnam ne dit pas que les noms d’espèce et de substance naturelle n’ont pas de sens, mais il insiste sur le fait que si leurs sens sont des entités cognitives, ils ne déterminent pas la référence. Certainement les locuteurs ont « à l’esprit » quelque chose en association avec ces mots : s’il s’agit de locuteurs compétents, ils ont « à l’esprit » un ensemble d’informations (que Putnam appelle stéréotype) considérées socialement nécessaires pour une utilisation adéquate du mot. Le stéréotype associé à “tigre” inclut le fait d’être un carnivore, d’avoir certaines dimensions, le pelage rayé jaune et noir, etc. On peut se demander si, également pour les noms propres, il existe un équivalent du stéréotype : si l’on considère socialement nécessaire d’associer à “Napoléon Bonaparte” l’idée d’un général français, qui conquit quasiment toute l’Europe au début du dix-neuvième siècle, etc. De fait, le problème n’a pas été posé, probablement parce qu’il semble non naturel de considérer ce genre d’informations comme faisant partie de la compétence linguistique.

Une autre catégorie à propos de laquelle on a parlé de référence directe ce sont les indexicaux. Le phénomène de l’indexicalité est extrêmement répandu dans le langage. Il concerne en premier lieu des mots comme “je”, “tu”, “ici”, “là”, “maintenant”, “hier”, etc. dont la référence dépend du contexte dans lequel ils sont utilisés. Mais il concerne également, par exemple, la dimension du temps verbal : la vérité ou la fausseté d’un énoncé temporalisé dépend, en général, du moment de son émission. “Mitterand sera élu président” est vrai avant mai 1981 et faux en 1997.

Dans quel sens les lemmes indexicaux (“je”, “tu”, etc.) ont une référence directe ? Nous observons tout d’abord que, tout comme les noms propres selon Kripke, ce sont des désignateurs rigides : étant donné un contexte, leur référence est la même dans tous les mondes possibles. Par exemple “je”, utilisé par un certain locuteur dans une circonstance déterminée, se réfère à lui dans tous les mondes possibles. Si j’écris maintenant “j’aurais pu être archéologue”, je suis en train d’imaginer un monde dans lequel Diego Marconi, et personne d’autre, est archéologue.

Deuxièmement, un indexical n’est pas synonyme d’une expression non indexicale (et il est généralement difficile d’en trouver un synonyme, même indexical). Par exemple, “je” n’est pas (comme on pourrait le croire) synonyme du “locuteur du contexte” (Napoli, 1992 : 420-421) : cette expression est une expression non rigide, qui se réfère à des individus différents dans des mondes différents (dans ce contexte, quelqu’un d’autre aurait pu parler à ma place), tandis que, comme nous venons de le voir, le mot “je” est rigide (étant donné un contexte). En général, les indexicaux ne peuvent être remplacés par d’autres expressions dans les contextes de croyance : « Quelqu’un peut croire qu’ici et maintenant nous avons une journée magnifique sans croire que le 5 novembre dans la banlieue de Turin puisse être une journée magnifique, parce qu’il peut ne pas connaître la date ni même le lieu où nous nous trouvons » (Napoli, 1992 : 418 n). Cet aspect – dit de l’« essentialité » des indexicaux – a été mis en évidence par J. Perry (1979) ; voir également Corazza-Dokic (1993).

Que l’on considère maintenant le phénomène suivant (Kaplan, 1977). L’énoncé “Je suis ici maintenant” est vrai dans chaque contexte dans lequel il est prononcé, et il est vrai « en vertu de la signification des mots », c’est-à-dire qu’il est analytique. Et pourtant, il n’exprime pas une vérité nécessaire : j’aurais pu tout aussi bien être ailleurs, et il n’est certainement pas nécessaire que je sois là maintenant. Nous pourrions dire que l’énoncé est vrai dans tous les contextes, mais, étant donné un contexte, il n’est pas vrai dans tous les mondes possibles. Par contraste, que l’on considère l’énoncé : “Je suis Diego Marconi” : il n’est certainement pas vrai dans tous les contextes, mais dans le contexte présent, il est vrai dans tous les mondes possibles. Il faut donc tenir compte, dans le cas des indexicaux, de deux paramètres ou indices qui contribuent à en déterminer la valeur sémantique : le contexte et le monde possible. D’après D. Kaplan, à un indexical sont associés un caractère et un contenu. Le caractère est une fonction de contextes à contenus : dans le cas de “je”, par exemple, le caractère est la règle qui associe à un contexte le locuteur de ce contexte. Le contenu, à son tour, est une fonction de mondes possibles à individus (lieux, moments, etc.) : le contenu de “je”, étant donné un contexte, associe à chaque monde possible un individu (et nous avons vu qu’il s’agit d’une fonction constante, qui associe toujours le même individu à tous les mondes possibles).

Le caractère d’un indexical s’identifie avec sa signification linguistique : celui qui connaît le français sait que “je” identifie le locuteur du contexte, “tu” identifie l’auditeur, etc. À la rigueur, le caractère n’est pas le sens de Frege, parce qu’il ne détermine pas de manière univoque la référence (Napoli, 1992 : 386) : il assigne à un indexical des référents divers dans des contextes divers. Toutefois, il ressemble au sens du fait qu’il est le contenu de la compétence linguistique, et la règle qui détermine la référence (non pas de manière univoque, mais selon les contextes). Donc, quand on soutient que les indexicaux ont une référence directe, on ne veut pas dire qu’ils n’ont pas de signification linguistique (comme les noms propres) : on veut au contraire insister sur le fait que, comme les noms propres, ce sont des désignateurs rigides, et – encore une fois comme les noms propres – ils ne peuvent être remplacés par d’autres expressions sans altérer la valeur de vérité des énoncés dans lesquels ils apparaissent.

33. Sémantique cognitive.

Le paradigme dominant ne s’intéresse pas à la compréhension du langage conçue comme processus mental : son étude est considérée comme étant du ressort de la psychologie et non de la sémantique. Le but de la sémantique, pour le paradigme dominant, c’est de déterminer systématiquement les conditions de vérité des énoncés d’un langage, indépendamment de la manière dont elles sont déterminées elles-mêmes par tel ou tel locuteur, et finalement tout aussi indépendamment du fait qu’elles lui soient connues, ou même accessibles (la position de Putnam (1975) peut être considérée comme un cas extrême de cette indifférence au problème de l’accessibilité des conditions de vérité ; voir supra, § 32). On a vu (§ 23) que la position de Dummett est, à cet égard, différente : par définition, les significations doivent être accessibles à un locuteur compétent, et la théorie de la signification doit être une théorie de la compréhension. Toutefois, Dummett continue de concevoir (frégéennement) les significations comme univoquement déterminées de la même manière pour tous les locuteurs, et il est très éloigné – tout comme Frege et Wittgenstein – de préoccupations de type psychologico-cognitif. Son problème c’est d’identifier des significations « absolues » de manière telle qu’elles soient en principe accessibles à un esprit fini. En revanche, au cours des années soixante-dix on avança différentes critiques concernant le paradigme dominant, qui vont dans la direction d’une révision draconienne de la théorie sémantique dans un sens cognitif (entendant par là, pour le moment, que la sémantique devait accorder une place aux notions d’« élaboration mentale » et de « représentation mentale » des significations). Les critiques les plus importantes concernent les attitudes propositionnelles et la notion de conditions de vérité.

On a vu (§ 7, 15) comment les contextes d’attitude propositionnelle ont représenté une limite à l’adéquation descriptive des sémantiques élaborées dans le cadre du paradigme dominant. Il s’est avéré très difficile, sinon impossible d’identifier les valeurs sémantiques des expressions du langage de manière telle que les contextes de la forme “X croit que p”, “X sait que p”, etc. s’avèrent compositionnels. Il semble que, étant donné deux énoncés quelconques :

(25) Georges croit que (sait que, se demande si, etc.) p

(26) Georges croit que (sait que, se demande si, etc.) q

où q coïncide avec p hormis que du fait où l’on a p à la place de q (p et q étant deux expressions de même valeur sémantique), il n’est jamais possible d’inférer (26) de (25). Pour donner un autre exemple de cette ancienne difficulté, on peut considérer comme vrai

(27) Les Babyloniens ne savaient pas que Hespéros est Phosphoros ;

mais ce serait faire tort aux Babyloniens de penser qu’il était également vrai que

(28) Les Babyloniens ne savaient pas que Hespéros est Hespéros.

Et pourtant, pour la théorie de Kripke, “Hespéros” et “Phosphoros” ont la même valeur sémantique (ayant la même référence).

Naturellement, les choses changent si, par exemple, nous ajoutons (29) à (25) :

(29) Georges sait que a et b sont synonymes.

L’inférence de (26) est alors pleinement justifiée (sur cette discussion voir Partee, 1979). Il semble donc qu’il y ait un lien entre l’incapacité du paradigme dominant à fournir des conditions de vérité correctes pour des énoncés comme (25) et (26) et son indifférence aux bagages cognitifs de sujets auxquels est attribuée une compétence linguistique. Pour le paradigme, les significations que Georges (ou n’importe quelle autre personne) attribue à p et à q, les relations inférentielles que Georges reconnaît, etc. ne peuvent entrer dans la détermination des valeurs sémantiques de (25) et (26) et de leurs constituants. Mais le traitement des attitudes propositionnelles semble nécessiter cela précisément.

L’autre critique importante concerne la notion de conditions de vérité. Dans les sémantiques du paradigme dominant, les conditions de vérité des énoncés complexes sont en dernière analyse reconduites aux valeurs sémantiques (intensions, par exemple) des constituants atomiques c’est-à-dire des mots. Les intensions des mots, par ailleurs, sont déterminées de manière simplement virtuelle : on suppose qu’il « y ait » une fonction qui assigne à chaque mot son intension, mais cette fonction n’est nullement décrite. On en spécifie simplement le type logique : nous savons, par exemple, que l’intension de “chat” est une fonction de mondes possibles à ensembles, mais nous ne savons pas comment la distinguer de l’intension de “livre”, qui est également une fonction de mondes possibles à ensembles. Comme l’a observé Johnson-Laird (1983 : 172), « on aimerait bien savoir quelle information est contenue dans le “corps” de la fonction qui correspond à l’intension d’un prédicat, c’est-à-dire qu’est-ce qui doit être calculé pour spécifier les individus qui possèdent la propriété [exprimée par le prédicat] » ; mais la sémantique ne répond pas à cette question.

L’absence de spécifications des valeurs des constituants atomiques a pour conséquence que les conditions de vérité des énoncés s’avèrent à leur tour déterminées de manière seulement virtuelle. La sémantique dominante, fondée sur le concept de conditions de vérité, n’est pas en mesure de spécifier véritablement les conditions de vérité de la plus grande partie des énoncés : dans un certain sens, elle ne sait pas faire la distinction entre la signification de “Le chat est sur le tapis” et celle de “Le livre est sur la table”. On peut penser – avec Partee, 1981 – que cette difficulté se résout simplement en ajoutant à la théorie une sémantique lexicale, qui aurait pour tâche de spécifier les valeurs sémantiques des constituants atomiques ; tandis que le traitement de la sémantique structurelle, c’est-à-dire de la manière dont les valeurs sémantiques des expressions complexes dépendent de celles de leurs constituants, resterait l’apanage des méthodes traditionnelles. Mais la construction de cette partie lexicale de la sémantique ne semble pas banale. Il faut noter que l’on ne peut penser résoudre le problème simplement en ajoutant à une sémantique structurelle un ensemble de postulats de signification (§ 16), parce que – comme l’a observé également B. Partee (1981 : 79) – les postulats de signification ne sont nullement suffisants pour déterminer de manière univoque la référence entendue des expressions atomiques d’un langage. Si ce que l’on entend reconstruire c’est la signification que les énoncés atomiques, et les mots qui en sont les constituants, ont pour un locuteur compétent, il semble nécessaire d’invoquer le rapport entre langage et monde en tant que médiatisé par la perception et par l’action : un concept qui est étranger au paradigme dominant, et qui va dans la direction d’une analyse de la compréhension comme processus cognitif.

Le problème de la signification lexicale a été mis en évidence par la recherche en Intelligence Artificielle. À partir des années soixante-dix, on a construit de nombreux systèmes d’élaboration automatique du langage naturel (pour un panorama mis à jour, voir Gazdar, 1993) : des systèmes qui répondent à des questions formulées dans une langue naturelle, qui résument des textes, qui traduisent d’une langue dans une autre, etc. Il est clair que le problème d’une représentation explicite de la signification des mots ne peut être mis entre parenthèses quand il s’agit de simuler une compétence sémantique complète : un système artificiel doit savoir inférer (par exemple) “Il y a quelques pachydermes à la maison” de “J’ai vu quatre éléphants dans le salon”, et cela nécessite qu’il connaisse – de quelque manière – la signification, ou des aspects de la signification de “éléphant”, “quatre”, “salon”, “voir”. La recherche en Intelligence Artificielle a produit différentes méthodes de représentation de la signification des mots : les plus répandues sont les réseaux sémantiques et les frames. Dans les versions les plus développées, les réseaux sémantiques sont équivalents à des systèmes de postulats de signification commandés par une logique de premier ordre. Les frames (Minsky, 1975) sont au contraire une forme de représentation non reconductible à celles traditionnelles. Voici un exemple de frame possible associé au mot “tigre” :

Dans un frame, les valeurs sont des valeurs possibles qu’une propriété peut assumer ; la valeur par défaut est la valeur qui est attribuée automatiquement à une propriété en absence d’informations plus précises. Les valeurs possibles représentent la possibilité de variation des propriétés des tigres possibles ; les valeurs par défaut représentent les propriétés du tigre typique. Un système de compréhension qui utilise des frames, devant interpréter un énoncé qui parle de tigres,

a) contrôlera que les propriétés que l’énoncé attribue au tigre dont on parle rentrent dans les valeurs possibles ;

b) attribuera la valeur par défaut lorsque l’énoncé n’attribue pas certaines propriétés ;

c) construira, de cette manière, le frame instancié relatif au tigre du discours (dans lequel à un certain individu x, tigre1, seront attribuées les propriétés explicitement attribuées par l’énoncé, plus les propriétés par défaut) ;

d) si nécessaire, il activera les procédures si nécessaire (dites démons). Par exemple, si l’énoncé parle d’un tigre de deux tonnes, il essaiera d’établir – en fonction du contexte – s’il ne s’agit pas par hasard d’un tigre artificiel, en pierre ou en marbre par exemple ;

e) il intégrera le frame instancié dans une représentation de l’énoncé dans lequel entreront d’autres frames instanciés (correspondant aux autres individus dont parle le discours, et aux situations de relation dans lesquels ces individus peuvent se trouver entre eux). Les frames en effet ne concernent pas seulement des classes d’individus, mais également des classes de situations, d’activités, etc.

Un frame ne se réduit pas à un ensemble traditionnel de postulats de signification, par la présence des valeurs par défaut. En effet, ceux-ci ne spécifient pas des relations rigides entre les mots (“Si x est célibataire, alors x n’est pas marié”), mais des relations qui valent en principe et en absence d’informations contraires. Un système à frames peut être interprété comme un ensemble de postulats de signification, à condition que ceci soit gouverné par une logique non classique (logique non monotone) qui règle les inférences par défaut.

L’Intelligence Artificielle (I.A.) a eu une influence considérable sur la philosophie du langage au cours des dix dernières années, mais n’a pas produit véritablement de théories sémantiques dignes de ce nom : même l’idée de sémantique procédurale, répandue en I.A. (Marconi, 1992 : 452-457), est plus une indication de recherche qu’une théorie au sens propre. Pourtant certains chercheurs travaillant aux frontières entres la linguistique, la psychologie cognitive, la philosophie et l’I.A. ont élaboré des théories ou des ébauches de théorie : il faut citer, à ce titre, les noms de Johnson-Laird (1983), Fauconnier (1985), Jackendoff (1983, 1987), Sperber et Wilson (1986), Lakoff (1987). Ces propositions, bien que très différentes, tendent à partager certaines idées de fond. En premier lieu, la sémantique doit être une théorie de la compréhension, et la compréhension est un processus cognitif, d’élaboration du langage par un esprit. En second lieu, le processus de compréhension implique la construction de représentations mentales. La nature précise de ces représentations (sans parler de leur réalisation neurocérébrale) est constamment sous-déterminée par les données (psychologiques ou neuro-physiologiques) : elles peuvent être conçues comme des formules d’un « langage de la pensée » (Fodor, 1975), un code mental qui partage de nombreuses caractéristiques des langages verbaux, ou au contraire (Johnson-Laird, Fauconnier) comme des modèles de l’état de choses décrit par l’énoncé qui tour à tour est compris, c’est-à-dire comme ensembles d’éléments en relation. Pour Johnson-Laird (1983 : 381 q.), par exemple, un modèle mental possible du texte : « A est à la droite de B ; C est devant B ; D est à gauche de C » est la structure

B      A

D      C

que l’on suppose de quelque manière réalisé dans l’esprit. Il faut noter que la structure mentale en question ne doit pas être confondue avec sa représentation symbolique, telle qu’elle est transcrite sur cette page : les représentations mentales – et c’est un des autres points largement partagé par les sémanticiens cognitivistes – ne sont pas des transcriptions symboliques, qui auraient à leur tour besoin d’être interprétées, mais sont elles-mêmes des interprétations : la construction d’une représentation, c’est la compréhension d’un énoncé. Les éléments d’une représentation ne sont pas des symboles en soi privés de signification, mais « des primitifs conceptuels innés, qui sont au fondement de notre capacité d’interpréter le monde, d’agir sur lui, etc. et sont “scellés” par rapport à l’analyse et à la description » (Marconi, 1992 : 463).

Enfin, les représentations mentales ne sont pas (comme les sens de Frege) des entités objectives, éventuellement accessibles aux esprits des locuteurs, mais sont (le résultat) des constructions qui se développent dans l’esprit de chaque locuteur ; et en ce sens, elles sont subjectives. La possibilité de la communication ne se fonde pas – comme dans le paradigme classique – sur l’objectivité des significations, mais sur la ressemblance des procédures d’élaboration du langage (Fauconnier, 1985 : 2 ; Jackendoff, 1983 : 31 ; Johnson-Laird, 1986 : 110) : en dernière analyse, sur la ressemblance des esprits et sur le partage d’un même monde.

34. Théories duelles

Ces dernières indications montrent de manière évidente à quel point la distance est grande entre la sémantique cognitive et le paradigme dominant et les théories de la référence directe. Malgré cela, les années quatre-vingt virent quelques tentatives d’intégration des instances cognitivistes à une idée centrale du référentialisme : celle pour laquelle la référence de mots comme “or” ou “tigre” est déterminée non pas par le concept d’or ou de tigre qu’un locuteur aurait « à l’esprit », mais par sa position objective dans le monde réel, et par la nature de celle-ci. Pour Oscar_TJ, citoyen de Terre Jumelle (§ 32), le mot “eau” se réfère – qu’il le sache ou non – à toute chose qui est XYZ, et seulement à cela, parce que le liquide qui paradigmatiquement s’appelle ”eau” sur Terre Jumelle est XYZ. Certains philosophes (Field, 1977 ; Loar, 1981 ; McGinn, 1982 ; Harman, 1982, 1987 ; Block, 1986 ; la position de Fodor, 1981, 1987, bien que différente, en est proche) ont souscrit à cette thèse, mais pas à la conclusion de Putnam pour qui « les significations ne sont pas dans la tête ». Pour ces théoriciens, une partie, ou un aspect de la signification est « dans la tête » : c’est cet aspect qui est à la base de la capacité d’un locuteur d’accomplir des inférences d’ordre sémantique, et qui détermine le rapport entre ses croyances, ses désirs et ses actions ; on lui a donné les noms de « rôle conceptuel » (Field, Harman), « signification restreinte » (Block), « rôle cognitif » (McGinn). C’est l’aspect de la signification effectivement disponible à un locuteur, qui entre comme ingrédient dans ses processus cognitifs conscients. A ses côtés, ces théoriciens placent l’aspect référentiel, qu’ils conçoivent plus ou moins comme Putnam. L’essentiel c’est qu’« aucune des deux contributions [à la signification d’un mot] ne suffit à déterminer l’autre, et tous deux sont nécessaires pour fixer le contenu d’ensemble » d’un mot (McGinn, 1982 : 211). Sur ce point, évidemment, les théoriciens des « deux aspects » divergent radicalement du paradigme frégéen (dans lequel le sens détermine la dénotation, l’intension détermine l’extension, etc.), en acceptant les critiques que Putnam et Kripke avaient faites à Frege et à ses épigones ; mais ils considèrent qu’il faut maintenir une composante « sens » (rôle conceptuel, etc.) parce qu’il faut bien que quelque chose de la signification d’un mot soit donné au locuteur et qui soit donc disponible pour ses élaborations cognitives. Au fond, Putnam lui-même avait anticipé cette admission, avec sa notion de stéréotype associé à un mot (§ 32).

Il était à prévoir que les théories duelles n’auraient pu satisfaire ni les référentialistes ni les cognitivistes. Un référentialiste comme Putnam, par exemple, a objecté que la composante « rôle conceptuel » n’a rien à voir avec la signification : si le rôle conceptuel d’“eau” a profondément changé au cours des siècles (en fonction des changements de nos connaissances chimiques, etc.), sa signification est toujours la même (Putnam, 1988 : 48-49). D’autre part, au moins certains théoriciens « duels » semblent peu sensibles à l’aspect cognitif – disons : intramental – de la détermination de la référence : la propre capacité d’un locuteur compétent d’appliquer le langage au monde réel ne semble pas faire partie de la composante « rôle conceptuel », et d’autre part elle ne coïncide pas avec la connaissance des références « objectives » dont parle Putnam, parce que nous ne sommes pas sûrs que ces derniers soient accessibles, non seulement à un locuteur particulier, mais pas même à la communauté linguistique dans son ensemble (Marconi, 1987). D’autres chercheurs ont observé que les théories duelles risquent de déterminer des conditions de vérité contradictoires pour le même énoncé (Fodor, 1987 : 82), selon qu’elles les déduisent de la composante « rôle conceptuel » ou de la composante référentielle ; ou encore qui ne sont pas en mesure de déterminer les conditions de vérité des énoncés, et donc ne peuvent servir à une théorie de la communication (Lepore et Loewer, 1987). Toutes ces critiques témoignent d’une tension irrésolue entre instances cognitives, référentialistes et les derniers tenants du paradigme dominant.

35. Réformes internes au paradigme.

Dans les années quatre-vingt, deux propositions de sémantiques pour le langage naturel ont suscité quelque intérêt : la sémantique des situations de J. Barwise et J. Perry (1983) et la théorie de la représentation du discours (DRT) de H. Kamp (1981 ; exposée largement in Kamp et Reyle, 1993). Dans le cas de Kamp, il s’agit véritablement du traitement sémantique d’un fragment de langage naturel, que l’on peut comparer à une grammaire de Montague (§ 17) ; dans l’autre cas – Barwise et Perry – la proposition n’est pas suffisamment précise pour permettre une comparaison, mais leur intention est de fournir le cadre théorique pour un tel traitement. À la différence de la sémantique cognitive, ces deux propositions restent en quelque sorte à l’intérieur du paradigme dominant (bien que Barwise et Perry insistent sur le caractère alternatif de leur théorie, et Kamp souligne les implications cognitives de la sienne). Des deux programmes de recherche, celui de Kamp semble aujourd’hui le plus vivace, mais nous évoquerons tout d’abord la sémantique des situations. Il faut noter, en tout cas, que toutes deux ont donné lieu à de très nombreuses recherches, théoriques et applicatives (en particulier dans les milieux de l’I.A.).

Au début des années quatre-vingt, on était largement convaincu – ce qui n’est plus le cas aujourd’hui – que le problème des attitudes propositionnelles (§ 15, 33) provenait essentiellement du fait que les discriminations de signification dont les théories en question étaient capables, n’étaient pas suffisamment « affinées ». Dans une sémantique des mondes possibles, si deux énoncés p et q sont vrais dans les mêmes mondes, ils ont la même valeur sémantique : et pourtant un sujet peut croire que p sans croire que q, parce que la différence entre p et q – que la théorie est incapable de saisir – est significative pour son état épistémique. De manière analogue, si deux prédicats s’appliquent aux mêmes objets dans tous les mondes possibles, ils ont la même valeur sémantique (= expriment la même propriété) ; et pourtant, quelqu’un peut penser qu’un certain champignon est une chanterelle sans penser que c’est une girolle. Et ainsi de suite. Il s’agissait donc – c’est du moins ce qu’il semblait – de repenser les valeurs sémantiques des énoncés (et par conséquent ceux de leurs constituants) de manière à saisir tous les contenus informatifs qui peuvent « faire une différence » pour les états épistémiques d’un sujet. C’est ce qu’ont proposé Barwise et Perry. Dans la sémantique des situations, la référence d’un énoncé déclaratif n’est pas (comme dans la tradition frégéenne) une valeur de vérité, mais une situation, une entité structurée qui « copie » l’énoncé, de manière très semblable à la façon dont les états de choses de Wittgenstein (§ 10) étaient des copies isomorphes des énoncés qui en étaient l’image. Aux prédicats du langage correspondent des relations et des propriétés qui sont considérées comme des entités primitives, et non – comme dans la sémantique des mondes possibles – des constructions fondées sur des individus et des mondes possibles (avec la conséquence que si à deux prédicats correspond la même construction, leur valeur sémantique est la même). Cette plus grande articulation devrait rendre possible un traitement adéquat des attitudes propositionnelles. Malheureusement, Barwise et Perry n’en ont jamais proposé un, c’est pourquoi il est difficile d’évaluer la théorie justement là où elle devrait donner la meilleure preuve de son bien-fondé.

L’appareil formel de la sémantique des situations est en même temps compliqué et imprécis ; en outre, la théorie a été et est toujours en évolution. C’est pourquoi il est difficile d’en présenter un exposé synthétique. Nous nous contenterons d’introduire les concepts principaux, en nous fondant sur Barwise et Perry, 1983 (pour un exposé plus complet, voir Bonomi, 1987 : 87-110, voir également Barwise, 1989). Une séquence de constituants est formée par une relation n-aire et par n objets : par exemple <à droite de, a, b>. Un type de situation est un ensemble de couples <séquence de constituants, valeur de vérité> : par exemple,

{<< à droite de, a, b >, Vrai>, << à gauche de, a, c >, Faux>}

est le type de situation dans laquelle a est à droite de b et non à gauche de c. Un état de choses est un couple constitué d’une position et d’un type de situation ; par exemple,

< en p : {<< à droite de, a, b >, Vrai>, << à gauche de, a, c >, Faux>}>.

Dans les sémantiques des mondes possibles, un énoncé est généralement évalué par rapport à un indice <monde possible, moment dans le temps> et à un contexte, qui spécifie un locuteur, un auditeur, un objet indiqué, un lieu d’émission de l’énoncé, etc. L’introduction des contextes est indispensable pour évaluer des énoncés contenant des expressions indexicales (§ 32), comme “Je t’ai prêté le livre de sa mère”. Dans la sémantique des situations, les contextes (dits situations de discours) sont des situations comme les autres : plus précisément, des états de choses dans lesquels sont spécifiés (au moins) un locuteur et un énoncé émis. La signification linguistique d’un énoncé déclaratif, pour Barwise et Perry (1983 : 15, 19, 120-121), est une relation entre des situations de discours (que Barwise et Perry appellent également “émissions”, utterances) et des situations en général : par exemple, la signification de “Je suis assis” est la relation qui subsiste entre une situation de discours d et une situation s si et seulement si il se trouve une position p et un individu a tels qu’en d, a est en train de parler en p, et en s, a est assis en p. En d’autres termes, la signification de “Je suis assis” est l’ensemble des couples de la forme << en p : < parle, a >, Vrai>, en p : <est assis, a >, Vrai >>.

Barwise et Perry présentent la sémantique des situations comme une alternative radicale à la sémantique d’origine frégéenne. Toutefois, ils maintiennent les aspects essentiels du paradigme dominant : la compositionnalité des valeurs sémantiques (1983 : 130), l’antimentalisme (1983 : 42), et au fond, l’idée même que la signification d’un énoncé est donnée par ses conditions de vérité (l’interprétation d’un énoncé, pour Barwise et Perry, c’est la classe des situations qui le satisfont). Certes, ils n’ont pas recours à la notion de monde possible, qui comporte de nombreux inconvénients : mais elle a aussi des avantages qui sont particulièrement évidents dans le traitement de la modalité, et Barwise et Perry n’ont pas proposé d’alternative sur ce point. La sémantique des situations semble donc une proposition interne au paradigme, particulièrement difficile à évaluer là où elle s’éloigne des solutions qui prévalent, comme celles offertes par la sémantique des mondes possibles.

La proposition de Kamp part elle aussi d’un problème bien connu de l’analyse du langage naturel. Les pronoms dits « personnels » ont différentes fonctions dans une langue comme le français : ils fonctionnent quelquefois comme des variables quantifiées comme dans (30) :

(30) Tout homme aime les femmes qui l’aiment,

dont la structure sémantique peut être saisie par

(31) ("x) (homme(x) Æ ("y)((femme(y) & aime (y,x)) Æ aime (x, y))).

D’autres fois, ils fonctionnent comme des termes dénotatifs, comme en (32) :

(32) Klaus possède Greta. Il la bat.

(32) est un exemple d’anaphore (pronominale) : “il” et “la” se réfèrent respectivement à Klaus et à Greta ; leur référence est médiée par leur coréférence à leurs antécédents anaphoriques, les noms propres “Klaus” et “Greta”.

Il y a toutefois une autre fonction des pronoms (Geach, 1962) que l’on ne peut assimiler aux deux autres. On peut en donner un exemple en (33)

(33) Si Klaus possède un âne, il le bat.

Intuitivement, les conditions de vérité de (33) sont exprimées par la formule de premier ordre suivante :

(34) ("x)((âne(x) & possède (Klaus, x)) Æ bat (Klaus, x)).

Toutefois, de l’avis d’un grand nombre de chercheurs (34) n’est pas une formalisation naturelle de (33). En effet, le syntagme nominal un âne semble posséder une valeur existentielle qui en (34) est perdue. Une formalisation plus naturelle de (33) serait quelque chose comme (35)

(35) ($x)(âne(x) & possède (Klaus, x)) Æ bat (Klaus, x).

Mais (35) est certainement inacceptable, parce que la dernière occurrence de la variable x est hors du cadre du quantificateur, et donc n’est pas coréférente aux autres (c’est comme si (35) disait : si Klaus possède un âne, alors Klaus bat x).

La théorie de Kamp se propose de représenter toutes les fonctions sémantiques des pronoms, y compris celles exemplifiées par (33) et (32). En tant qu’elle traite explicitement des cas d’anaphore interénonciative, la théorie est une des premières tentatives (avec celle de Johnson-Laird, 1983, qui, d’ailleurs lui ressemble par certains aspects) d’élaboration de représentations sémantiques de textes (et non seulement de simples énoncés), en intégrant les représentations des énoncés qui les composent conformément aux connexions réciproques que les locuteurs sont en mesure d’identifier. La théorie se compose de trois modules (comme celle de Montague, voir § 17) : (a) une syntaxe, qui produit des expressions bien formées de la langue ; (b) un algorithme de construction des représentations, dites structures de représentation du discours, DRS ; (c) une sémantique – dans le sens de la théorie des modèles, voir § 13 – qui interprète les DRS. Une DRS est une famille structurée de représentation du discours (DR), qui seulement dans les cas les plus simples n’est constitué que d’une simple DR. Par exemple la DRS correspondant à (33) est la suivante :

Le module sémantique assure que K(1) a les conditions de vérités « justes », c’est-à-dire celles exprimées par (34) ; tandis que l’algorithme de construction des DRS saisit la valeur existensielle exprimée par “un âne”. Le fait que le processus de construction des DRS respecte (dans ce cas comme dans d’autres) nos intuitions sur la manière dont un énoncé est élaboré dans le cours de sa compréhension, a incité Kamp lui-même (1981 : 282) à conjecturer une dimension cognitive de ses représentations : « Les structures que l’on peut supposer [...] que les locuteurs forment pour représenter des contenus verbaux sont, sinon formellement identiques, du moins très semblables aux représentations définies ici ». Ces mérites cognitifs peuvent être mis en doute : dans la DRT, la charge majeure de l’analyse sémantique du langage n’est pas portée par les procédures de construction des représentations, mais par le module que nous avons justement nommé “sémantique” ; de sorte que le moment du processus d’analyse auquel est attribué une réalité cognitive – la construction de la DRS – n’atteint pas réellement le niveau sémantique. Les DRS de Kamp ont plutôt la nature de formes logiques explicites, qui constituent un passage intermédiaire dans l’assignation des conditions de vérité aux énoncés d’un langage naturel : en cela, elles ressemblent aux formules de la “logique intensionelle” de Montague. Ce qui ne met nullement en doute les qualités de rigueur formelle et de relative simplicité de la théorie de Kamp qui lui ont assuré son succès récent.

BIBLIOGRAPHIE

M. Andronico, D. Marconi, C. Penco (a cura di), Capire Wittgenstein, Marietti, Gènes 1988.

J. L. Austin, « Other Minds » (1946, puis in 1961 [tr.fr.]).

—— « Truth » (1950, puis in 1961 [tr.fr.]).

—— « A Plea for Excuses » (1956-1957, puis in 1961 [tr.fr.]).

—— Philosophical Papers, Clarendon Press, Oxford 1961 [tr. fr. L. Aubert et A. N. Hacker, Écrits philosophiques, Le Seuil, Paris 1994].

—— How to Do Things with Words, Oxford Univ. Press, 1962 [tr. fr. G. Lane, Quand dire c’est faire, Le Seuil, Paris 1970].

J. Barwise, The Situation in Logic, CSLI, Stanford 1989.

J. Barwise, J. Perry, Situations and Attitudes, MIT Press, Cambridge 1983.

A. Benmakhlouf, Gottlob Frege, logicien et philosophe, PUF, « Philosophies », Paris, 1997.

A. Bilgrami, « Pour le holisme sémantique » in Lire Davidson, (P. Engel éd.), l’éclat, Combas 1994.

N. Block, « An Advertisement for a Semantics for Psychology », Midwest Studies in Philosophy 10, 1986.

A. Bonomi (a cura di), La struttura logica del linguaggio, Bompiani, Milan 1973.

—— Eventi mentali, Il Saggiatore, Milan 1983.

—— Le immagini dei nomi, Garzanti, Milan 1987.

A. Bottani, C. Penco (a cura di), Significato e teorie del linguaggio, Angeli, Milan 1991.

J. Bouveresse, Le Mythe de l’intériorité. Expérience, signification et langage privé chezWittgenstein, éd. de Minuit, Paris 1976.

—— Herméneutique et linguistique, suivi de Wittgenstein et la philosophie du langage, L’éclat, Combas 1991.

R. Carnap, Der logische Aufbau der Welt, Meiner, Hamburg 1928.

—— « Überwindung der Metaphysik durch die logische Analyse der Sprache », Erkenntnis 1932.

—— Logische Syntax der Sprache, Vienne 1934 [éd. angl. Routledge & Kegan Paul, London, 1937].

—— Meaning and Necessity, Univ. of Chicago Press, Chicago 1947 [tr. fr. Signification et nécessité, Gallimard, Paris, 1997 (toutefois les nos de pages renvoient à l’éd. originale)].

—— « Meaning Postulates », Philosophical Studies 1952, 65-73, puis en appendice à Carnap 1947 (à partir de l’éd. de 1955).

—— « Intellectual Autobiography », in A. Schilpp (éd.), The Philosophy of Rudolf Carnap, The Library of Living Philosophers, 1963.

P. Casalegno, « Il paradigma di Frege », in Santambrogio (a c. di) 1992.

—— Filosofia del linguaggio, La Nuova Italia Scientifica, Rome 1997.

P. Casalegno, D. Marconi, « Alle origini della semantica formale », in Santambrogio (a c. di) 1992.

G. Chierchia, S. McConnell-Ginet, Meaning and Grammar, MIT Press, Cambridge 1990.

A. Church, « A Formulation of the Logic of Sense and Denotation », in P. Henle, H. M. Kallen, S. K. Langer (éds.), Structure, Method and Meaning, Liberal Arts Press, New York 1951a.

—— « The Need for Abstract Entities in Semantic Analysis », Proceedings of the American Academy of Arts and Sciences 80, 1951b.

J.-P. Cometti, Philosopher avec Wittgenstein, PUF, Paris 1996.

—— « Le pragmatisme, de Peirce à Rorty », in M. Meyer, La philosophie anglo-saxonne, PUF, Paris 1994.

V. Cook, Chomsky’s Universal Grammar, Blackwell, Oxford 1988.

E. Corazza et J. Dokic, Penser en contexte. Le phénomène de l’indexicalité : la controverse John Perry & Gareth Evans, l’éclat, Combas 1993 [contient également John Perry : « Frege et les démonstratifs » et Gareth Evans « Comprendre les démonstratifs »].

D. Davidson, « Truth and Meaning », Synthese 1967, puis in Davidson 1984.

—— « Semantics for Natural Languages », in B. Visentini (a cura di), Linguaggi nella società e nella tecnica, Comunità, Milan 1970 ; puis in Davidson 1984 [tr. fr.].

—— « Radical Interpretation », Dialectica 1973, puis in Davidson 1984 [tr. fr.].

—— « On the Very Idea of a Conceptual Scheme », Proceedings and Addresses of the American Philosophical Association, 14. 1974 ; puis in Davidson 1984 [tr. fr.].

—— Inquiries into Truth and Interpretation, Oxord Univ. Press, Oxford 1984 [tr. fr. P. Engel, Enquêtes sur la vérité et l’interprétation, éd. Jacqueline Chambon, Nîmes 1993].

—— « A Nice Derangement of Epitaphs », in E. Lepore (ed.), Truth and Interpretation. Perspectives on the Philosophy of D. Davidson, Blackwell, Oxford 1986.

M. Di Francesco, Introduzione a Russell, Laterza, Rome-Bari 1990.

D. Dowty, R. Wall, S. Peters, Introduction to Montague Semantics, Reidel, Dordrecht 1981.

M. Dummett, The Justification of Deduction, 1973a, puis in Dummett 1978.

—— Frege : Philosophy of Language, Duckworth, Londres 1973b.

—— Truth and Other Enigmas, Duckworth, Londres 1978.

—— Ursprünge der analytischen Philosophie, Suhrkamp, Francfort s. M. 1988 [tr. fr. M.-A. Lescourret, Les origines de la philosophie analytique, Paris, Gallimard 1991].

P. Engel, La norme du vrai, Gallimard, Paris 1989.

—— Davidson et la philosophie du langage, PUF, Paris 1994.

—— Philosophie et psychologie, Gallimard, Paris 1996.

—— (éd.), Lire Davidson, l’éclat, Combas 1994.

G. Evans, « The Causal Theory of Names », Proceedings of the Aristotelian Society, Suppl. Vol. XLVII, 1973 ; puis in S. P. Schwartz (éd.), Naming, Necessity, and Natural Kinds, Cornell Univ. Press, Ithaca 1977.

G. Fauconnier, Mental Spaces, MIT Press, Cambridge 1985.

H. Field, « Logic, Meaning, and Conceptual Role », Journal of Philosophy 1977, 379-409.

J. Fodor, The Language of Thought, Harvester, Hassocks 1975.

—— Representations, Harvester, Brighton 1981.

—— Psychosemantics, MIT Press, Cambridge 1987.

G. Frege, Ecrits logiques et philosophiques, tr. fr. C. Imbert, Le Seuil, Paris 1971.

—— Begriffschrift, Nebert, Halle 1879.

—— Funktion und Begriff, H. Pohle, Iéna 1891 ; [tr. fr., in Écrits logiques et philosophiques, cit.].

—— « Über Begriff und Gegenstand », Vierteiljahrschrift für wissenschaftliche Philosophie 1892a (16), 192-205 ; [tr. fr., in Écrits logiques et ..., cit.].

—— « Über Sinn und Bedeutung », Zeitschrift für Philosophie und philosophische Kritik 1892b (100), 25-50 [tr. fr. in Écrits logiques et ..., cit.].

—— Grundgesetze der Arithmetik begriffschriftlich abgeleitet, Vol. 1, H. Pohle, Iéna 1893 [rééd. anastatique Olms, Hildesheim 1962].

—— Logik (1897), Nachgelassene Schriften Vol. 1, Meiner, Hamburg 1969.

—— « Lettre à Ph. Jourdain », s. d. [1914], in Wissenschaftlicher Briefwechsel, Meiner, Hamburg 1976.

—— « Der Gedanke. Eine logische Untersuchung », Beiträge zur Philosophie des deutschen Idealismus 1918, 143-157 [tr. fr. in Ecrits logiques et philosophiques, cit.].

—— Logische Untersuchungen. Dritter Teil : Gedankengefüge, Beiträge zur Philosophie des deutschen Idealismus, 1923-1926, 36-51.

M. Frixione, Logica, significato e intelligenza artificiale, Angeli, Milan 1994.

H. G. Gadamer, Wahrheit und Methode, Mohr, Tübingen 1960 [tr. fr. Vérité et méthode, Le Seuil, Paris 1996].

G. Gazdar, « The Handling of Natural Language », in D. Broadbent (éd.), The Simulation of Human Intelligence, Blackwell, Oxford 1993.

P. Geach, Reference and Generality, Cornell Univ. Press, Ithaca 1962.

R. Gibson, The Philosophy of W. V. Quine. An Expository Essay, University of South Florida, Tampa 1982.

P. Gochet, « L’empirisme relatif de Quine », in M. Meyer, La philosophie anglo-saxonne, PUF, Paris 1994.

K. Graham, J. L. Austin, A Critique of Ordinary Language Philosophy, Harvester, Hassocks 1977.

H. P. Grice, « Meaning », in Philosophical Review, 1957 (66), 377-88 ; puis in Grice 1989.

—— « Utterer’s Meaning, Sentence-Meaning, and Word-Meaning », in Foundations of Language, 1968 (4), 225-42 ; puis in Grice 1989.

—— « Utterer’s Meaning and Intentions », in Philosophical Review 1969 (78), 147- 77 ; puis in Grice 1989.

—— « Logic and Conversation », in P. Cole, J. L. Morgan (éds.), Syntax and Semantics. Speech Acts, Academic Press, New York 1975, 41-58 ; puis in Grice 1989.

—— Studies in the Way of Words, Harvard Univ. Press, Cambridge 1989.

I. Hacking, Why Does Language Matter to Philosophy ?, Cambridge 1975.

G. Harman, « Conceptual Role Semantics », Notre Dame Journal of Formal Logic 1982, 252-6.

—— « (Nonsolipsistic) Conceptual Role Semantics », in New Directions in Semantics, Academic Press, Londres 1987, 55-81.

R. Jackendoff, Semantics and Cognition, MIT Press, Cambridge 1983.

—— Consciousness and the Computational Mind, MIT Press, Cambridge 1987.

Ph. Johnson-Laird, Mental Models, Cambridge Univ. Press, Cambridge 1983.

—— « How is Meaning Mentally Represented ? », in Versus 1986, 99-118.

H. Kamp, « A Theory of Truth and Semantic Representation », in J. Groenendijk, T. Janssen, M. Stokhof (éds.), Formal Methods in the Study of Language, Mathematisch Centrum, Amsterdam 1981.

H. Kamp et U. Reyle, From Discourse to Logic, Kluwer, Dodrecht 1993.

D. Kaplan, « Demonstratives », 1977, in J. Almog, J. Perry, H. Wettstein (éds.), Themes from Kaplan, Oxford Univ. Press 1989.

A. Kenny, Wittgenstein, Penguin Press, Londres 1973.

S. Kripke, « A Completeness Theorem in Modal Logic », Journal of Symbolic Logic 1959 (24), 1-14.

—— « Naming and Necessity », in G. Harman, D. Davidson (éds.), Semantics of Natural Language, Reidel, Dordrecht e Boston 1972 ; puis en volume, avec une nouvelle introduction, Blackwell, Oxford 1980 [tr. fr. F. Récanati, La logique des noms propres, Minuit, Paris 1982].

—— Wittgenstein on Rules and Private Language, in I. Block (éd.) Perspectives on the Philosophy of Wittgenstein, Oxford, Blackwell, 1981, pp. 238-312 ; puis en volume, Oxford, Balckwell, 1980 [tr. fr. T. Marchaisse, Règles et langage privé. Introduction au paradoxe de Wittgenstein, Le Seuil, Paris 1996].

S. Laugier, L’Anthropologie logique de Quine, Vrin, Paris 1992.

G. Lakoff, Women, Fire, and Dangerous Things, Chicago Univ. Press, Chicago 1987.

P. Leonardi, « La filosofia del linguaggio ordinario », in Santambrogio (a cura di) 1992.

E. Lepore, B. Loewer, « Dual Aspect Semantics », in New Directions in Semantics, Academic Press, London 1987.

S. Levinson, Pragmatics, Cambridge Univ. Press 1983.

D. Lewis, « General Semantics », Synthese 1970, 18-67.

L. Linsky (éd.), Reference and Modality, Oxford Univ. Press 1971.

—— Le problème de la référence, Le Seuil, Paris 1974.

B. Loar, Mind and Meaning, Cambridge Univ. Press, Cambridge 1981.

G. Lolli, « Logica e intelligenza artificiale », Sistemi Intelligenti 1991, 7-36.

J. Lyons, Semantics, 2 voll., Cambridge Univ. Press, Cambridge 1977.

D. Marconi, « Che cos’è la teoria della verità di Tarski ? », Teoria 1984, 75-95.

—— « Two Aspects of Lexical Competence », Lingua e Stile 1987, 385-95.

—— « Semantica cognitiva », in Santambrogio (a c. di) 1992.

M. Mariani, « Gli atteggiamenti proposizionali », in Santambrogio (a c. di) 1992.

C. McGinn, « The Structure of Content », in A,Woodfield (éd.), Thought and Object, Clarendon, Oxford 1982.

M. Minsky, « A Framework for Representing Knowledge », in P. Winston (éd.), The Psychology of Computer Vision, McGraw Hill, New York 1975, 211-77.

M. Meyer (éd.), La philosophie anglo-saxonne, PUF, Paris 1994.

R. Montague, « Universal Grammar », Theoria 1970, 373-98 ; puis in Montague 1974.

—— Formal Philosophy, ed. by R. Thomason, Yale Univ. Press, Londres 1974.

E. Moriconi, « La teoria del significato di M. Dummett », in Santambrogio (a cura di), 1992.

C. Morris, Foundations of the Theory of Signs, The University of Chicago Press, Chicago, 1938.

E. Napoli, « Riferimento diretto », in Santambrogio (a cura di), 1992.

B. Partee, « Semantics. Mathematics or Psychology ? », in R. Bauerle, U. Egli, A. von Stechow(eds.), Semantics from Different Points of View, Springer, Berlin-New York 1979.

—— « Montague Grammar, Mental Representations and Reality », in S. Kanger, S. Öhman (éds.), Philosophy and Grammar, Reidel, Dordrecht 1980.

C. Penco, « Wittgenstein. Dopo il Tractatus », in Santambrogio (a cura di), 1992.

Ch. Perelman, De la justice, Off. de Publ., Bruxelles 1945.

J. Perry, « The Problem of the Essential Indexical », Nous 1979, 3-22.

E. Picardi, « Über Sinn und Bedeutung : un’esposizione elementare », Lingua e Stile, Parte I 1989, 331-64, Parte II 1990, 159-99.

—— Linguaggio e analisi filosofica, Pàtron, Bologne 1992.

H. Putnam, « Dreaming and “depth grammar” », 1962, puis in Putnam 1975, 304-24.

—— « The meaning of “meaning” », in Putnam 1975.

—— Mind, Language and Reality, Philosophical Papers Vol. 2, Cambridge Univ. Press 1975.

—— Raison, vérité et histoire, tr. fr. A. Gerschenfled, Minuit, Paris 1984.

—— Representation and Reality, MIT Press, Cambridge 1988 [tr. fr. C. Tiercelin, Représentation et réalité, Gallimard, Paris 1990].

W. V. O. Quine, « Truth by Convention », in Philosophical Essays for A. N. Whitehead, 1936 ; puis in The Ways of Paradox, Random House, New York 1966, 70-99.

—— « Two dogmas of Empiricism », in Philosophical Review, 1951, puis in From a logical point of view, Cambridge, Harvard, U. P., 1953 [tr. fr. P. Jacob in De Vienne à Cambridge, P. Jacob éd., Gallimard, Paris 1980].

—— Word and Object, MIT Press, Cambridge Mass. 1960 [tr. fr. P. Gochet, Le mot et la chose, Flammarion, Paris 1977].

—— « Reference and Modality », in From a Logical Point of View, Harper & Row, New York 1961.

—— Ontological Relativity and Other Essays, Columbia Univ. Press, New York 1969 [tr. fr. J. Largeault, Aubier-Montaigne, Paris 1977].

F. Récanati, Les énoncés performatifs, éd. de Minuit, Paris, 1981.

—— Direct Reference, Basil Blackwell, Oxford, 1993.

F. Rivenc, « Logique, langage et philosophie », in M. Meyer (éd.), La philosophie anglo-saxonne, PUF, Paris, 1994.

R. Rorty (éd.), The Linguistic Turn, Univ. of Chicago Press, Chicago 1967.

—— Philosophy and the Mirror of Nature, Princeton Univ. Press 1979 [tr. fr., T. Marchaisse, L’homme spéculaire, Le Seuil, Paris 1990].

—— Conséquences du pragmatisme, tr. fr. J.-P. Cometti, Le Seuil, Paris 1993.

—— « Le pragmatisme, Davidson et la vérité » in Science et solidarité, tr. fr. J.-P. Cometti, l’éclat, Combas 1990.

E. Rosch, « Wittgenstein and Categorization Research in Cognitive Psychology », in M. Chapman, R. A. Dixon (éds.), Meaning and the Growth of Understanding, Springer, Berlin 1987.

B. Russell, « On Denoting », Mind 1905, 479-93 ; [tr. fr. J.-M. Rey, in Ecrits de logique philosophique, PUF, Paris, 1989].

—— The Problems of Philosophy, London, William and Norgate, 1912 ; [tr. fr. F. Rivenc, Payot, Paris, 1989] (les références renvoient à l’éd. Oxford University Press, Oxford 1959.).

—— Essais philosophiques, tr. fr. F. Clémentz et J.-P. Cometti, PUF, Paris, 1997.

—— The Philosophy of Logical Atomism (1918-19), Open Court, La Salle Ill. 1985[tr. fr. in Ecrits de logique philosophique, cit.].

—— Introduction to Mathematical Philosophy, Allen & Unwin, London 1919 [tr. fr. G. Moreau, Introduction à la philosophie des mathématiques, Payot, Paris, 1970 (une nouvelle traduction due à F. Rivenc a paru en 1991)].

M. Santambrogio, « Introduzione » à la tr. it. de Dummett 1978.

—— (a cura di), Introduzione alla filosofia analitica del linguaggio, Laterza, Roma-Bari 1992.

—— « Quine », in Santambrogio (a cura di) 1992.

M. Sbisà (a cura di), Gli atti linguistici, Feltrinelli, Milano 1978.

M. Schlick, « The Future of Philosophy », 1932, in Rorty (éd.) 1967.

—— « Meaning and Verification », Philosophical Review 1936, puis in Philosophicals Papers, vol. 2, Reidel, Dordrecht 1979.

J. R. Searle, « Proper Names », Mind 1958, 166-73 ; puis in Searle 1969.

—— Speech Acts, Cambridge Univ. Press, Londres 1969 [tr. fr. H. Pauchard, Les Actes de langage, Hermann, Paris 1985].

—— « Indirect Speech Acts », in P. Cole, J. L. Morgan, Syntax and Semantics. Speech Acts, Academic Press, New York 1975a.

—— « A Taxonomy of Illocutionary Acts », in K. Gunderson (éd.), Language, Mind, and Knowledge, Univ. of Minnesota Press, Minneapolis 1975b.

M. Seymour, « Discours indirect et citation », in Lire Davidson (P. Engel éd.), L’éclat, Combas, 1994.

D. Sperber, D. Wilson, Relevance. Communication and Cognition, Blackwell, Oxford 1986 [tr. fr. D. Sperber et A. Gerschenfeld, La pertinence. Communication et cognition, éd. de Minuit, Paris, 1989].

R. Stalnaker, « Pragmatics », in G. Harman, D. Davidson (éds.), Semantics of Natural Language, Reidel, Dordrecht 1972.

A. Tarski, Pojecie prawdy w jezykach nauk dedukcyjnych [Le concept de vérité dans les langages des sciences déductives], Varsavia 1933.

—— « The semantic Conception of Truth and the Foundations of Semantics », in Philosophy and Phenomenology Research, 1944, 4, pp. 341-376 ; puis in Linski (éd.) Semantics and the philosophy of Language, Univ. of Illinois Press, 1952.

—— Logic, Semantics, Metamathematics, Oxford Univ, Press, Oxford 1956 (IIe éd. Hackett, Indianapolis, 1983) ; [tr. fr. sous la dir. de G.-G. Granger, in Logique, sémantique, métamathématique, Armand Colin, Paris 1972].

L. Wittgenstein, Tagebücher 1914-1916, Blackwell, Oxford 1961 (IIe éd. 1979) [tr. fr. G.-G. Granger, Carnets, Gallimard, Paris 1971].

—— Tractatus logico-philosophicus, Routledge & Kegan Paul, Londres 1922 [nouvelle tr. fr. G.-G. Granger, Gallimard, Paris 1994].

—— Philosophische Bemerkungen (1929-1930), Blackwell, Oxford 1964 [tr. fr. J. Fauve, Remarques philosophiques, Gallimard, Paris 1975].

—— Wittgenstein und der Wiener Kreis (1929-32), notes rédigées par F. Waismann, Blackwell, Oxford 1967 [tr. fr. G. Granel, Wittgenstein et le Cercle de Vienne, TER, Mauvezin 1991].

—— Philosophische Grammatik (1930-33), Blackwell, Oxford 1969 [tr. fr. M.-A. Lescourret, Grammaire philosophique, Gallimard, Paris 1980].

—— Blue Book (1933-34), Blackwell, Oxford 1958 [nouvelle tr. fr. M. Goldberg et J. Sackur, Le Cahier bleu et le Cahier brun, Gallimard, Paris 1997].

—— Brown Book (1934-35), Blackwell, Oxford 1958 [tr. fr. voir supra].

—— Philosophische Untersuchungen (I : 1945 ; II : 1947-49), Blackwell, Oxford 1953 [dont il existe une “traduction” parue en 1961 sous le titre Investigations philosophiques].

index des noms propres

Andronico, M. : 73
Aristote : 10
Austin, J. L. : 14, 16, 18, 22, 65, 66, 80-85, 92, 97

Barwise, J. : 122-125
Block, N. : 120
Bonomi, A. : 58, 123
Bouveresse, J. : 66, 75

Carnap , R. : 12, 18, 19, 21,-23, 44-47, 53-60, 62, 82, 89, 90, 92, 104
Casalegno, P. : 23, 28, 50, 57, 95
Chierchia, G. : 62
Chomsky, N. : 10, 17, 19, 64, 65
Church, A. : 43, 53, 56, 89
Condillac 9
Cook, V. : 17
Corazza, E. : 112

Davidson, D. : 94, 99, 100-103
Di Francesco, M. : 35
Dokic, J. : 112
Dummett, M. : 16, 19, 21, 47, 67, 76-79, 113

Engel, P. : 11, 102
Evans, G. : 108

Fauconnier, G. : 119, 120
Field, H. : 120
Fodor, J. : 47, 76, 119-121
Frege, G. : 9-13, 18, 19, 21-24, 27-34, 36, 39, 40, 41, 53-56, 77-79, 88, 90, 98, 99, 104-106, 112, 113, 120, 121
Frixione, M. : 104

Gadamer, H. G. : 12
Gazdar, G. : 116
Geach, P. : 125
Gibson, R. : 98
Graham, K. : 80
Grice, H. P. : 85-88

Hacking, I. : 19
Harman, G. : 120
Hintikka, J. : 61
Humboldt, 9, 10
Hume, D. : 10

Jackendoff, R. : 119, 120
Jakobson, R. : 19
Johnson-Laird, P. : 115, 119, 120, 126

Kamp, H. : 122, 125-128
Kanger, S. : 61
Kant, I. : 58
Kaplan, D. : 112
Kenny, A. : 40, 68
Kripke, S. : 22, 60-62, 73, 92, 104-109, 111, 114, 121

Lakoff, G. : 119
Langford, 61
Leibniz, G. W. : 9, 54, 57
Leonardi, P. : 80, 86, 87
Lepore, E. : 122
Levinson, S. : 87
Lewis, D. : 58, 61
Linsky,L. : 92
Loar, B. : 120
Locke, J. : 9
Loewer, B. : 122
Lolli, G. : 104
Lyons, J. : 59

Malcolm : 15
Marconi, D. : 48, 50, 73, 100, 118, 119, 121
Mariani, M. : 58
McConnell-Ginet, S. : 62
McGinn, C. : 120, 121
Mill, J. S. : 9
Minsky, M. : 117
Montague, R. : 19, 60, 62-65, 104, 105, 122, 126, 128
Moriconi, E. : 80
Morris, C. : 52, 84

Napoli, E. : 108, 111, 112
Neurath, R. : 44
Nietzsche, F. : 10

Partee, B. : 115, 116
Penco , C. : 73, 76
Perelman, Ch. : 20
Perry, J. : 112, 122,-125
Picardi, E. : 16, 80
Platon 9, 28
Putnam, H. : 15, 104, 109, 110, 113, 120, 121

Quine, W. v. O : 15, 22, 47, 53, 58, 60, 65, 66, 82, 89, 90, 92-99, 101-103
Récanati, F. : 85, 109
Reyle, U. : 122
Rorty, R. : 15, 18
Rosch, E. : 71
Russell, B. : 11, 13, 16, 19-22, 25, 32-36, 39, 40-42, 98, 104, 106
Ryle, G. : 14, 18, 65

Santambrogio, M. : 77
Saussure, F. de : 19
Schlick, M. : 14, 44-46
Searle, J. : 85, 86, 107
Socrate 14
Sperber, D. : 119
Stalnaker, R. : 85
Strawson, P. : 65

Tarski, A. : 18, 19, 47-54, 60, 61, 89, 99, 100, 101, 102

Wilson, D. : 119
Wisdom, J. : 66
Wittgenstein, L. : 10, 11, 13, 14, 18, 19, 21, 22, 28, 32, 36, 37, 39, 40-47, 51-54, 65-78, 81, 94, 98, 107, 113, 123
von Wright, R. : 61

M. Ripley s’amuse